根据实验数据整理出数学模型,并根据数学模型作出某些预测,是很多学科都需要面临的问题。 所以,用计算机处理实验数据也是比较重要的基本技能。
本文以对某二极管的电压-电流曲线的测量为例,介绍如何解决两个问题的方法:
- 如何根据给定数据和模型,求取模型上的参数(拟合);
- 如何(利用或者不利用1的结果),求在某个未被测量的点上函数的斜率。
所以这篇文章的内容只是对这些问题进行肤浅的介绍。 实际上,除了拟合出的模型外,更重要的是对误差的估计。 本文将重点介绍技术方法,而非这方面的数学理论, 希望能根据这些介绍,帮助读者熟悉能解决这些问题的计算机工具。
1. 背景
1.1 假设的实验内容
使用如下数据作为例子,假设如下数据为由某型号的二极管测量到的电压-电流曲线(又称伏安特性曲线)。
| 点 | U/V | I/A | 点 | U/V | I/A | 点 | U/V | I/A |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000 | 0.0000 | 10 | 0.6490 | 0.2244 | 19 | 0.7027 | 1.2509 |
| 2 | 0.1802 | 0.0000 | 11 | 0.6580 | 0.2947 | 20 | 0.7119 | 1.7024 |
| 3 | 0.2704 | 0.0000 | 12 | 0.6671 | 0.3920 | 21 | 0.7210 | 2.3197 |
| 4 | 0.3605 | 0.0000 | 13 | 0.6756 | 0.5128 | 22 | 0.7254 | 2.9605 |
| 5 | 0.4511 | 0.0018 | 14 | 0.6804 | 0.5461 | 23 | 0.7345 | 3.8915 |
| 6 | 0.4955 | 0.0045 | 15 | 0.6848 | 0.6921 | 24 | 0.7482 | 6.0382 |
| 7 | 0.5403 | 0.0126 | 16 | 0.6898 | 0.8165 | 25 | 0.7542 | 7.8235 |
| 8 | 0.5866 | 0.0405 | 17 | 0.6937 | 0.9265 | 26 | 0.7594 | 8.4940 |
| 9 | 0.6321 | 0.1370 | 18 | 0.6984 | 1.0842 | - | - | - |
1.2 目标
我们希望回答两个问题:
- 可否找到一条描述如上测量数据点的曲线,如果有,是什么;
- 独立于问题1,能否找到在
U=0.7000 V这个点上的伏安特性曲线的切线斜率。
2. Plan A: 将数据根据某模型拟合,并根据模型求斜率
这个方法的思想是,相信有一个曲线可以代表已经测量的东西(这里是一个二极管)。 查阅相关资料之后了解到肖克利二极管方程就是这样一个模型:
\[ I = I(V_{D}) = I_{s} (e^{\frac{V_{D}}{nV_{T}}} - 1) \]
其中,
- \(I_{s}\) 称为饱和电流,范围在\(10^{-12}\)到\(10^{-6}\)A;
- \(V_{T}\) 称为热电压,在20摄氏度室温约为 0.025 V;
- \(n\) 称为发射系数,在1到2之间(对于理想二极管为1)。
因为以上3个参数都可以在实验过程中认为是常数,所以整个模型就简化成了2个参数(a, b)和1个变量(U)的方程:
\[ I = I(U) = a (e^{\frac{U}{b}} - 1) \]
我们的目的就是,寻找合适的(a,b)取值,使得上述模型 尽可能地接近 我们的测量结果。
“尽可能地接近”?
“尽可能地接近”,说明我们需要一个评判模型和实测数据是否接近的标准。
中学数学中我们学到的最小二乘法,就是这样的评判标准之一。
这个评判标准,是将模型(上文提到的\(I=I(U)\))依次在全部已知测量点\(U_i\)(给定的二极管两端电压)上给出的预测结果\(I(U_i)\)和实测结果\(I_i\)相减, 所有差值的平方再求和。这个总和\(\Sigma\)越小,就说明模型越接近实测数据:
\[ \Sigma = \Sigma [I(U_i) - I_i]^2 \]
这样,本文的问题就成了寻找合适的(a,b),使得二变量函数\(\Sigma=\Sigma(a,b)\)取最小值的问题。
这个问题我们现在不想进行理论上的讨论。我们直接在下文介绍用计算机工具来寻找(a,b)的方法。
2.1 使用 GNU Octave 求解
GNU Octave是一个可以替代 MATLAB 的开源软件,功能和后者几乎一致,但却可以免费下载和使用。
GNU Octave的官方网站上可以下载到供Windows使用的安装包。
供Linux使用的软件包,可以直接通过各发行版的软件源安装。
2.1.1 认识Octave
Octave启动后的界面类似下图:
界面可以自己定义,左侧一般包括文件浏览器、工作区等几个窗口,右侧则是命令窗口。
文件浏览器可以查看和编辑和当前工作有关的文件。
一般启动Octave的目录是工作目录,
这个目录中的文件,比如各种.m结尾的程序文件,是Octave可以直接找到的。
所以一般推荐对一个专门的问题单独设定一个工作目录。
工作目录可以通过界面中的当前目录工具栏修改。
工作区中列出的是当前状态下程序所存储的变量、它们的类型和值。
命令窗口是用户向Octave输入指令,获取数据的交互界面。
Octave的指令其实就是用来输入、输出、处理数据等的程序语言。
只不过通过命令窗口的输入是一条一条语句依次进行的,
而通过.m文件加载的代码是自动批量执行的。
2.2.2 输入数据
和很多程序语言一样,我们所谓的输入数据,就是一个赋值的语句。
Octave作为处理数值问题的语言,比较专业的一点在于变量的值可以是矩阵(或者行、列向量)。 下面的语句,将测量数据作为两个行向量输入:
xi = [0, 0.1802, 0.2704, 0.3605, 0.4511, 0.4955, 0.5403, 0.5866, 0.6321, 0.649, 0.658, 0.6671, 0.6756, 0.6804, 0.6848, 0.6898, 0.6937, 0.6984, 0.7027, 0.7119, 0.721, 0.7254, 0.7345, 0.7482, 0.7542, 0.7594];
yi = [0, 0, 0, 0, 0.0018, 0.0045, 0.0126, 0.0405, 0.137, 0.2244, 0.2947, 0.392, 0.5128, 0.5461, 0.6921, 0.8165, 0.9265, 1.0842, 1.2509, 1.7024, 2.3197, 2.9605, 3.8915, 6.0382, 7.8235, 8.494];可以在命令窗口直接输入上述命令。之后可以使用xi+回车这样的方式,查看输入。
2.2.3 定义我们的模型
我们使用下面的一条语句定义模型:
model = @(a,b,x) a * (exp(x / b) - 1);这一句话的意义很丰富:
@(a,b,x)指明接下来要定义一个表达式函数,它接受3个变量(a,b,x);a * (exp(x / b) - 1)指明我们要使用的表达式,即上文所述的肖特基二极管方程;model = ...意为将定义的一句话函数命名为model。
2.2.4 定义最小二乘法的评判函数
定义的语句如下,仍然是一句话:
sumerr = @(p) sum( ( model(p(1), p(2), xi) - yi ) .^ 2 );这里比上面的表达更复杂了一点:
sumerr = @(p),说明这个评判函数的名字将要叫做sumerr,接受输入为p;sum( ( model(p(1), p(2), xi) - yi ) .^ 2 )是这个函数的具体内容,我们将这些括号成对拆开看:model(p(1), p(2), xi)是一个调用model进行计算的语句。- 注意到我们使用了
p(1),p(2)这样的写法,这说明我们希望p在输入时应该是一个至少2个元素的行/列向量。p(1)就是这个向量中的第1个值的意思。 xi,见2.2.2,本身就是一个行向量。 所以这句语句的运行结果,是对xi中的每一个元素进行分别计算,得到一个和xi维度一致(这里是1行26列)的结果矩阵。
- 注意到我们使用了
(model(...) - yi)这个括号,是对model(...)调用的结果矩阵和yi矩阵进行相减。这里遵循矩阵减法,亦即是分别相减。(...) .^ 2是对上面一个得到的减法数组的每项都进行平方。sum(....)是对上面得到的平方数组的每项求和。
2.2.5 开始计算
搜索(a,b)参数只需要一个命令fminsearch,用法如下:
p0 = [0, 0.025];
p = fminsearch(sumerr, p0);第一句话是给定初始值p0, 这样Octave就知道需要如法炮制把一个2元素的行向量送给sumerr来求结果。
根据前面的叙述,读者可能还记得p(1)是a,p(2)是b:
a代表饱和电流,是个很小的值,接近0。
b代表指数函数的系数,我们取常温下接近热电压0.025 V的值作为初始值。
第二句话调用搜索函数fminsearch,搜索使sumerr函数取最小值的p。搜索到的结果传给p变量。
2.2.6 计算结果
上面介绍的步骤,可以组成一个完整的程序,然后取名为mycalc.m存放在工作目录中。
完整的内容:
%% 输入数据
xi = [0, 0.1802, 0.2704, 0.3605, 0.4511, 0.4955, 0.5403, 0.5866, 0.6321, 0.649, 0.658, 0.6671, 0.6756, 0.6804, 0.6848, 0.6898, 0.6937, 0.6984, 0.7027, 0.7119, 0.721, 0.7254, 0.7345, 0.7482, 0.7542, 0.7594];
yi = [0, 0, 0, 0, 0.0018, 0.0045, 0.0126, 0.0405, 0.137, 0.2244, 0.2947, 0.392, 0.5128, 0.5461, 0.6921, 0.8165, 0.9265, 1.0842, 1.2509, 1.7024, 2.3197, 2.9605, 3.8915, 6.0382, 7.8235, 8.494];
%% 定义模型
model = @(a,b,x) a * (exp(x / b) - 1);
%% 定义最小二乘评估标准
sumerr = @(p) sum( ( model(p(1), p(2), xi) - yi ) .^ 2 );
%% 计算
p0 = [0, 0.025]; % 搜索起点
p = fminsearch(sumerr, p0); % 开始搜索调用程序,在命令窗口中进行操作如下:
octave:1> mycalc % 回车,调用上面的mycalc程序
octave:2> p % 回车,显示p的值
p =
9.0078e-08 4.1618e-02
如果已经安装了optim包,还可以继续计算模型在给定位置的斜率:
octave:3> pkg load optim; % 加载optim包
octave:4> deriv(@(x) model(p(1), p(2), x), 0.7000)
ans = 43.648
2.2 使用 Python 求解
Python 是一门功能强大但又十分简明易懂的编程语言。使用Python可以节约大量的时间。
2.2.1 安装 Python
Python在很多Linux发行版已经是标准配置。这里不再赘述。
在Windows也是可以使用Python的,除了官方的Python安装包之外,还可以使用一些第三方的专门打包,比如 Anaconda。这些打包注重科学计算方面的应用,会附带下面将要用到的Python库。
否则,您需要自己安装numpy和scipy这两个库。
2.2.2 使用 Python 进行计算
Python的使用方式同Octave类似,都提供命令行输入和程序执行。
区别在于Python本身并没有自带一个图形界面,您需要通过Windows的命令行或者类似的方式启动它。 Python命令行启动后类似这样:
直接在这里就可以输入编程语句。
如果要执行一个Python程序,在启动Python时给出程序名称即可:
$ python myprogram.py
2.2.3 示例计算
我们首先看使用Python进行上述计算的程序。下面的代码可以保存成一个文件,然后如上一节所述交Python调用。
#!/usr/bin/env python
import numpy as np
from scipy.optimize import curve_fit
xi = [0, 0.1802, 0.2704, 0.3605, 0.4511, 0.4955, 0.5403, 0.5866, 0.6321, 0.649,
0.658, 0.6671, 0.6756, 0.6804, 0.6848, 0.6898, 0.6937, 0.6984, 0.7027, 0.7119,
0.721, 0.7254, 0.7345, 0.7482, 0.7542, 0.7594]
yi = [0, 0, 0, 0, 0.0018, 0.0045, 0.0126, 0.0405, 0.137, 0.2244, 0.2947, 0.392,
0.5128, 0.5461, 0.6921, 0.8165, 0.9265, 1.0842, 1.2509, 1.7024, 2.3197, 2.9605,
3.8915, 6.0382, 7.8235, 8.494]
model = lambda x,a,b: a * (np.exp(x * 1.0 / b) - 1)
res = curve_fit(model, xi, yi, p0=[0, 0.025])
ps = res[0]
print ps
print (model(0.7001, *ps) - model(0.7000, *ps)) / (0.0001) # 手动计算斜率主要思想和Octave方式一样,只不过我们使用了scipy.optimize这个软件包中的curve_fit函数来代替我们定义最小二乘法求值的过程:
model = lambda x,a,b: ...这一句是lambda表达式, 和Octave里@(x) ...的语法一样,都是定义一个一句话函数,然后交给叫做model的变量留存。- 但是根据
curve_fit的要求,函数第一个参数需要是自变量本身,所以参数表顺序是x,a,b。
- 但是根据
curve_fit求出的极小值有多个,需要按照合理范围取舍。 如果需要,可以在程序结尾附加一句print res查看。 根据上述程序的数据,我们取res[0],即第一个结果为拟合结果。- 计算斜率一行
model(0.7000, *ps)中使用*ps方式将ps的结果(一个二维数组)“打散”成2个变量调用函数。 这是Python的语法特性之一。
上面程序的运行结果如下:
$ python test.py
[ 7.20720803e-11 2.97441081e-02]
40.3472792927
$
发现求得的(a,b)参数和Octave给出的不一样。但切线斜率还是很接近。
2.3 比较
我们将Octave和Python的结果作一比较:
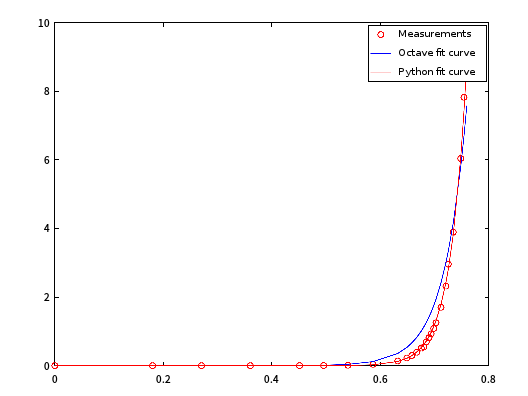
根据以上方法求得的拟合结果,Python的结果显然比Octave的好。 这并不是说两种软件有什么区别,可能还和默认的一些参数,比如迭代次数等的选取有关。
3. Plan B: 通过插值求解
对于很多问题,很可能并不存在一个解析形式的数学模型。这时使用插值求解就还是很有必要。
插值(Interpolation),根据某种方法在已知的数据点之外,求未知点的值。 插值问题是数值方法中的一个重要的话题,这里仅仅列出几种方法,比较下它们的好坏。
技术上,使用Python的scipy软件包,可以很快地实现各种插值。
我们就用这个作为演示。
使用下列代码作为后续程序的开头部分。
# -*- coding: utf-8 -*-
#!/usr/bin/env python
import numpy as np # 导入用于方便数值计算的库 numpy,简称为 np
from scipy.interpolate import * # 从 scipy.interpolate 库中导入全部(插值功能)
xi = [0, 0.1802, 0.2704, 0.3605, 0.4511, 0.4955, 0.5403, 0.5866, 0.6321, 0.649,
0.658, 0.6671, 0.6756, 0.6804, 0.6848, 0.6898, 0.6937, 0.6984, 0.7027, 0.7119,
0.721, 0.7254, 0.7345, 0.7482, 0.7542, 0.7594] # 定义 x 上各点
yi = [0, 0, 0, 0, 0.0018, 0.0045, 0.0126, 0.0405, 0.137, 0.2244, 0.2947, 0.392,
0.5128, 0.5461, 0.6921, 0.8165, 0.9265, 1.0842, 1.2509, 1.7024, 2.3197, 2.9605,
3.8915, 6.0382, 7.8235, 8.494] # 定义对应各 x 的 y 测量结果
# 定义一个从 0 到 0.76 的数字序列,一共包含500项均分点
# 我们将用 sxi 系列上的 x 值绘出插值曲线
sxi = np.linspace(0, 0.76, 500)3.1 拉格朗日插值
拉格朗日插值是一种“耍赖”的插值方法,即对于给定的N个数据点,构建一个次数足够的多项式,使它们的根都穿过这些点:
两个点构成一条直线,三个点构成一条抛物线,依次类推……
这种做法虽然可以保证所有的点都会被穿过,但在点很多时,点之间却可能出现很大的误差,称为龙格(Runge)现象。 Wikipedia上对此的示例图如下:
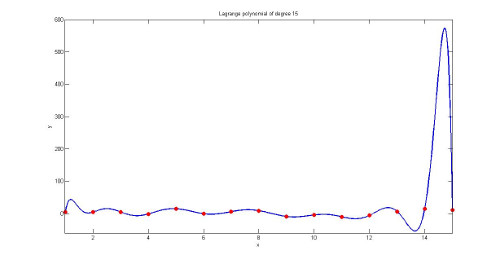
使用拉格朗日插值,在scipy.interpolate包中提供了lagrange函数,它只需要两个输入,分别是各点的x值和y值:
lagrange_curve = lagrange(xi, yi) # 计算一个可以用来插值的曲线
lagrange_curve_at_point = lagrange(0.7) # 用这个方法可以计算插值曲线在 x = 0.7 的值由于对本实验数据拟合结果过于糟糕(龙格现象严重)(读者可以自己验证),我们就放弃这个插值方案。
3.2 样条插值
3.2.1 一次样条插值
所谓一次样条,就是一条将各个数据点都连接起来的折线,两相邻点之间为直线段。
这种插值方法很简单易懂,用手也可以进行计算。例如假设有\(x_0\), \(x\), \(x_1\) 三个点,满足\(x_0 < x < x_1\),端点上的对应y值分别是\(y_0\), \(y_1\), 则:
\[ y(x) = y_0 + \frac{x-x_0}{x_1-x_0}(y_1-y_0) \]
而被计算点\(x\)的处的切线斜率,也就是通过它之前和之后一点\(x=x_0\)和\(x=x_1\)的连线的斜率。
用这种方法手工计算\(U=0.7000V\)处的斜率,由实验数据,有:
- \(U_0=0.6984V\), \(I_0=1.0842A\)
- \(U_1=0.7027V\), \(I_1=1.2509A\)
故
\[ \frac{\mathrm{d}I}{\mathrm{d}U} \approx \frac{I_1-I_0}{U_1-U_0} = \frac{1.2509-1.0842}{0.7027-0.6984} \Omega^{-1}= 38.76 \Omega^{-1} \]
当然也可以使用Python进行计算:
tck1 = splrep(xi, yi, k=1) # splrep: 根据 xi, yi 计算一次样条(k=1)的参数
evspline1 = splev(sxi, tck1) # splev: 根据 tck1 的参数,对给定列表 sxi 的值分别计算插值结果
ev1 = splev([0.7000, 0.7001], tck1) # 或者我们在 splev 的第一个参数中给出我们要的 x 点,就能得到这一点的插值 y
didu1 = (ev1[1] - ev1[0]) / 0.0001 # 计算从 x = 0.7000 到 x = 0.7001的斜率均值
print didu1 # 38.7674418605为了运行的效率,计算分两步进行:第一步是求出描绘这个样条曲线的参数,存储到tck1这个变量中。
第二步是将tck1的参数和用户给定的一系列点sxi或者[0.7000]一起输入到splev函数,求出对应的全部插值结果。
这种两步计算,节省了在多次插值时重复计算样条参数的过程。
3.2.2 三次样条插值
3.2.1的插值结果对于曲线来说还是不够令人满意。 一般来说,我们希望将各个数据点用光滑的曲线连接起来,再计算结果。
那么什么叫光滑的曲线呢?
如果我们用多项式描绘两个相邻数据点之间的连线,那么直线就是一阶的多项式。 直线连线可以保证在端点\(x_0\), \(x_1\)上折线的连续性,即\(P(x_0) = P(x_1)\)。
如果我们提高要求,不止端点上函数本身连续,而且函数的一阶导数也连续,即 \(P’(x_0) = P’(x_1)\),换句话说一个端点两端的曲线斜率一致,这样就作出了二次样条。
进一步要求函数的二阶导数连续,\(P’‘(x_0) = P’‘(x_1)\),就作出了三次样条。
和一次样条插值很类似,我们都使用splrep和splev来计算插值:
tck3 = splrep(xi, yi, k=3) # k=3: 三次样条
evspline3 = splev(sxi, tck3)
ev3 = splev([0.7000, 0.7001], tck3)
didu3 = (ev3[1] - ev3[0]) / 0.0001
print didu3 # 37.4438805463.2.3 比较一次和三次样条的插值结果
将3.2.1和3.2.2所绘制的样条,与测量数据放到同一个图中放大查看,比较区别:
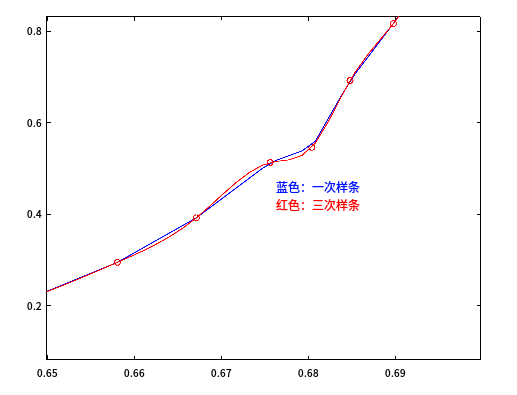
看到两种插值方式在本例中区别不大。但即使是三次样条也没有出现龙格现象的问题。
3.3 通过对平滑数据拟合的样条进行插值
scipy.interpolate.UnivariateSpline提供了一个并不一定穿过数据点,
但构建尽可能接近它的样条曲线的方法。笔者尚不清楚背后的数学原理。
用法如下:
uvs = UnivariateSpline(xi, yi, s=0.1) # s 的取值见下面说明
didh4 = (uvs(0.7001) - uvs(0.7000)) / 0.0001 # 求在 x = 0.7000 附近的导数
print didh4 # 38.5919662219代码中的s是一个描述要将数据平滑到什么程度的数字,有点类似方差。
数字越小,样条越接近数据点,但只要不是0, 就不会完全通过。
这个参数将会控制生成的样条中的节点,使得算出的方差小于给定值。
这对于实验数据中有波动的情况是十分有益的,例如以s=0.1绘制样条,结果(细节)如下:
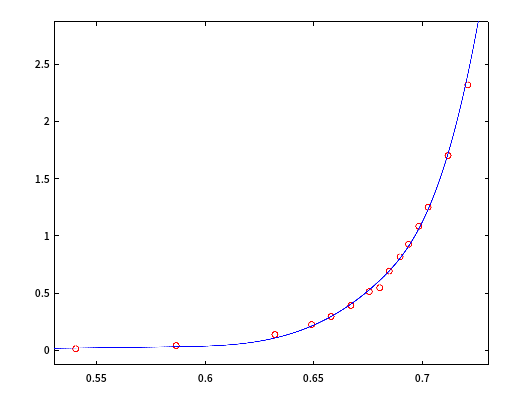
这种通过放弃一些点,使整体实验数据看起来更加平滑的方法,正是我们需要的。
4 总结
我们试着用Octave和Python对一次实验数据进行了分析。
对于有模型的情况,Octave和Python都很合适,可以用来寻找给定数学模型的参数。 在得到数学模型后,可以对其分析,获得诸如有关导数的信息。
对于没有模型的情况,可以使用Python的scipy包中interpolate子包的功能,
使用多种方式在实验数据中插值,得到未知点的数值和未知点附近的斜率等信息。
在后一种情况下,比较各种插值方式后,
我们发现,UnivariateSpline这个函数给出的平滑后的样条曲线,对实验数据的取舍较好,
适合描述本次实验结果的整体趋势,又不会因为细节而导致局部出现较大偏差,
是比较好的选择。