NERV负责人由于最近格瓦斯喝得较多,忽然想起用这种高耐压瓶子制作水火箭的可能。
的确,在NERV实验室早期的确做过这类实验。由于认识和技术原因,这类实验的收获也不大。 现在试图利用学到的一些本科知识,重新考虑这一装置。
结构设计
关于结构设计,NERV将在之后进行。现在只提出一些想法。
- 不依赖角度的飞行。
- 水火箭,利用高压气体将水喷射,获得反作用力飞行。由于水是流体,在飞行过程中,受到非牛顿参考系下的惯性力和重力的影响,其液面位置会变化。
- 水能被高压气体喷出的前提是,水浸没喷口。因为液面位置变化,这一前提并不一定能得到满足。
- 设计利用液压系统的蓄压瓶的原理,使用气球或者塑料袋(气球虽然自重比塑料袋高,但是可以附加额外的压力)充水,连接至喷口。充满水的气球在瓶中。 瓶中气球以外的部分,是高压空气。
- 这一设计的优点还有,可以使用相对简单的方式加工饮料瓶的盖子。气球通过管道连接到喷口,这一管道通过普通瓶盖即可(不需要是胶塞)。
- 此外,充气结构、发射时的触发结构,也可预料,变得简单。发射触发结构可以是释放喷口上的塞子。而喷口管道由于可以任意固定在任意位置(根据设计,可以不是瓶子的轴线上), 堵住它的方法也很灵活。
利用计算机程序模拟水火箭飞行
首先假设如下:
- 喷水速度由伯努利方程确定,取瓶内液面上一点和喷出水流中一点连线的流线,由压力差确定喷射速度。
- 喷流的静压为大气压。
- 瓶内气体的膨胀过程为绝热膨胀过程。忽略水喷射完毕后由于瓶内气体的喷射而产生的推力。
- 飞行中火箭的喷射力方向与其速度方向在同一直线,方向相反。
- 不计空气阻力。
由此,使用如下python程序模拟计算火箭飞行。
from math import *
timeDifference = 0.001
g = 9.8
k = 1.4
densityWater = 1000.0
volumeMax = 1.5 * 10**(-3)
emptyMass = 100.0 * 10**(-3)
nozzleArea = 0.0000503 # circle, D=8mm
initVolumeWater = 1.0 * 10**(-3)
initInnenPressure = 10.0 * 101325
initAngleHorizonal = pi / 2.0
##############################################################################
maxY = 0
maxX = 0
speedU, speedV = 0, 0
positionX, positionY = 0, 0
currentWaterVolume = initVolumeWater
currentInnenPressure = initInnenPressure
currentAirVolume = volumeMax - initVolumeWater
currentFlyAngle = initAngleHorizonal
currentTime = 0
while True:
if positionX > maxX:
maxX = positionX
if positionY > maxY:
maxY = positionY
currentRocketMass = currentWaterVolume * densityWater + emptyMass
waterExhaustSpeed = sqrt(2 * currentInnenPressure / densityWater)
exhaustedWaterVolume = waterExhaustSpeed * nozzleArea * timeDifference
currentWaterVolume -= exhaustedWaterVolume
newAirVolume = currentAirVolume + exhaustedWaterVolume
currentInnenPressure *= (currentAirVolume / newAirVolume) ** k
currentAirVolume = newAirVolume
thrust = 2 * nozzleArea * currentInnenPressure
if currentWaterVolume <= 0:
currentWaterVolume = 0
currentInnenPressure = 0
thrust = 0
thrustX = thrust * cos(currentFlyAngle)
thrustY = thrust * sin(currentFlyAngle)
# sum up forces
forceSumY = -currentRocketMass * g + thrustY
forceSumX = thrustX
# apply newton laws
accelerationY = forceSumY / currentRocketMass
accelerationX = forceSumX / currentRocketMass
speedU += accelerationX * timeDifference
speedV += accelerationY * timeDifference
positionX += speedU * timeDifference
positionY += speedV * timeDifference
# determine new fly angle
if speedU == 0:
currentFlyAngle = pi / 2
elif speedV == 0:
currentFlyAngle = 0
else:
currentFlyAngle = atan(speedV / speedU)
print currentTime, currentInnenPressure, currentFlyAngle / pi * 180, currentWaterVolume * 1000, positionX, positionY
if positionY <= 0:
break
currentTime += timeDifference
print 'maxHeight', maxY, 'maxDistance', maxX程序的########一行以上,除去第1行,为初值赋值。
在while True:的循环中,程序首先确定这一时刻的受力,然后据此确定加速度、速度和位置。
当火箭飞行的高度为负,亦即火箭再一次落地,程序停止。
为了了解这一程序计算的精确程度,需要进行如下实验。
时间步长无关性验证
对于很多计算机数值仿真的程序,其运行结果的准确性和所取时间步长或者网格精度有关。在精度较低的情况下,结果是不可信的。因此首先需要通过进行不同的精度选择,确定可以用的时间步长。timeDifference是程序在仿真时选取的时间步长变量。
下面的计算,假设有一个1.5 L的水火箭,自重100 g,喷嘴口径8 mm,内部水量初始为1.0 L,内部压力初始为1013250 Pa进行验证。
取射角90度,即竖直向上发射,可因此画出高度-时间曲线和剩余水量-时间曲线。分别取timeDifference的值为0.1 ms,1 ms,10 ms,100 ms绘制,如图:
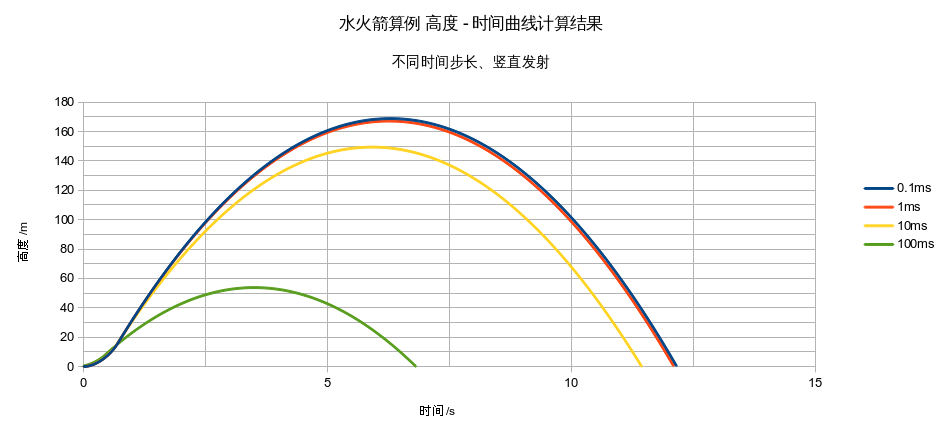
可以看到,在时间步长timeDifference取0.1 ms和1 ms时,计算结果吻合度较好。
即使timeDifference取为10 ms,计算结果虽然偏差稍大,也可以说趋势(在程序计算能力内,时间步长越小越精确)是正确的。
但是当时间步长取为100 ms,则出现明显偏差。
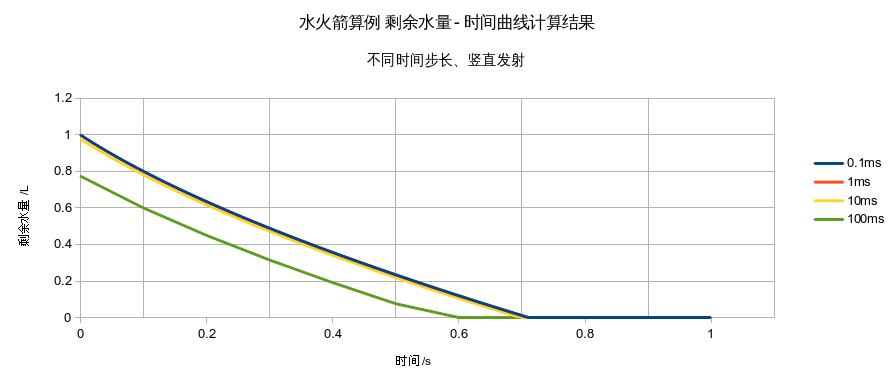
这一原因可以从剩余水量-时间曲线看出。从剩余水量-时间曲线首先可以分析出,只有当时间步长优于10 ms时,才有较高的准确度。
其次可以看出,在大约t=0.7s的位置,水耗尽。即这一水火箭的喷射过程持续只有0.7s或700ms。
这说明,水火箭的喷水加速过程是一个相对总飞行时间(如高度时间曲线所示,大于10s)比较迅速的过程,为此,需要有较高的计算精确度才能描述这一过程。
在使用10 ms的时间步长时,对这一过程进行了70次计算。但使用100 ms的话,就只有7次计算,误差很大。
此外发现,本程序仅在计算竖直方向时的精度较好,当初始射角非竖直时,计算结果的准确性即使在0.1 ms数量级的时间步长下也有明显偏差。
这里不附相关结果,读者可以自行用以上程序验证。在没有解决这一问题之前,使用本程序将仅进行对竖直射高的评估。
需要利用程序解答的问题
- 使用盐水或者酒精能否以及怎样对射程产生影响?
- 使用较小的喷口,延长喷射时间,能否和怎样对射程产生影响?
- 使用水和压力怎样的比例,能产生良好的射程?
(未完待续)