1. 实验报告概要
题目为“伽玛辐射功率和辐射功率测量”的核反应堆实习于2015年6月2日在德累斯顿工业大学进行。 实验的任务是,认识三个测量仪器的用法,使用这些仪器测量一个Cs-137放射源的伽玛辐射功率,以及测量各种材料对辐射的屏蔽能力。 从这些实验数据中,还需求出放射源的放射活度,和各种材料的衰减系数。
2. 基础知识
2.1 放射性和核辐射
放射性是一种关于原子或者材料的自然现象,其中有自发的以各种形式的能量辐射。这类能量的释放称为核辐射。
核辐射可以以粒子的动能形式释放出来,也可以以光量子的形式。按照这些能量的载体的类型来分类,可以将辐射分为如下几种:
\(\alpha\)辐射 释放的是一个氦原子核 \(_2^4\mathrm{He}\)。释放它的原子因此失去2个中子和2个质子。这种辐射极易屏蔽,例如只需要用一张厚纸。
\(\beta\)辐射 这种辐射在原子核内的核子发生变化时产生。常见的是一个中子变成了一个质子,(\(\beta^{-}\)辐射)。 这种情况下一个电子\( _{-1}^{0}\textrm{e} \)将会从核中被释放出来。在有些原子核,例如\(^{40}\textrm{K}\)中,还有一种相反的形式。 一个质子会变成一个中子,然后一个正电子\(_{1}^{0}\textrm{e}\)被释放(\(\beta^{+}\)辐射)。 \( \beta \)辐射可以用例如铝箔进行屏蔽。
中子辐射 这类辐射是关于中子的,它可以在核裂变的时候产生,例如正在运行中的核反应堆或者具有自发裂变特性的材料。 另一种可能是例如铍一样的轻核在受到外部的激发(通过\(\alpha\)粒子或者足够能量的\(\gamma\)光子)时发生的衰变。
\(\gamma\)辐射 这里一个被激发的原子核将它的能量以一个光量子的形式释放出来。这种辐射不是粒子,而是和可见光一类的辐射。 由于它具有很高的能力,\(\gamma\)辐射可以穿透很厚的物体,必须使用较重原子的材料(例如铅)进行屏蔽。
在本实验中,将使用的放射源是一个Cs-137源。这个放射源在进行\(\beta^-\)衰变的时候给出电子。 这样它产生的辐射首先是\(\beta^-\)辐射。然而还要注意的是,和很多其他的原子核一样, 在衰变之后,原子核还会处于一个较高的能态,它在跃迁到较低的相对稳定的能态时会通过\(\gamma\)辐射的形式释放其能量。 在Cs-137源中这种效应产生了很明显的\(\gamma\)辐射功率。
2.2 放射活度
考虑一群随着时间不断衰变的核素。 在任何一个时刻,都在剩余的原子核数量中,有固定的一个比例的原子核发生衰变。 这种这类核素的原子核的消失速度,就通过放射活度\(A\)来描述。
如果在一秒钟内,有一个原子发生了衰变,那么放射活度就是\(1\,\textrm{Bq}\)。 这个单位\(\textrm{Bq}\)于是说是很小的。 对于放射活度,相关的衰变定律描述了它随时间的变化规律:
\[ A=A_0 \cdot 2^{-t/T_{0.5} } \]
其中, \(T_{0.5}\)叫做半衰期,\(t\)是从起始开始计算的逝去的时间。 以在本实验中使用的Cs-137源为例,\(T_{0.5}=30.17\,\textrm{a}\)。 在1993年2月,测量的放射活度是 \(A_{2.1993}=0.26\,\textrm{GBq}\)。 考虑逝去的时间 \(t=(2015-1993)+(6-2)/12=22.33\,\textrm{a} \),可以得知当前的放射活度为:
\[ A_{6.2015}=A_{2.1993}\cdot 2^{ -t/T_{0.5} }=0.26 \times 2^{-22.33/30.17}=0.1556\,\textrm{GBq} \]
这应当和实验结果吻合,见4.1.3小节。
2.3 辐射功率
辐射剂量的功率描述了一个放射源的能量强度。它是剂量对时间的商。
如果一个物体,质量是\(1\,\textrm{kg}\),吸收了\(1\,\textrm{J}\)的核辐射能量, 它就受到了吸收剂量\(D\)为\(1\,\textrm{Gy}\)的辐射。 如果这个辐射过程是持续进行了一个小时完成的,那么吸收剂量的功率就是\(1\,\textrm{Gy/h}\)。
出于一些例如辐射防护的理由,需要了解辐射对于生物的影响。这不仅仅和吸收剂量相关,也取决于辐射的种类。 因此,各种吸收剂量需要对应与权重相乘,之后求和,得到等价剂量\(H\)。 它的单位是\(\textrm{Sv}\):
\[ H=\sum_i w_i D_i \qquad i=\alpha,\beta,\gamma,n \]
类似吸收剂量,对于等价剂量功率也有引入一个单位\(\textrm{Sv/h}\)。
权重\(w_{i}\)对于\(\beta\)和\(\gamma\)辐射都是1。 对于\(\alpha\)辐射,\(w_{\alpha}=20\)。对于中子辐射,\(w_n\)取值在5到20之间。 这样对于在实验中只处理\(\beta\)和\(\gamma\)辐射的时候,一个技巧就是,可以直接利用吸收剂量\(D\)的数值来替代等价剂量\(H\)。
吸收剂量在真空中的点状放射源情况下,是正比于放射活度\(A\),而与和放射源的距离\(r\)的二次方成反比:
\[ P=\frac{\mathrm{d}D}{\mathrm{d}t}=K\frac{A}{r^{2}} \]
其中,\(K\)是一个剂量常数。对于在本实验中使用的Cs-137源,\(K=92.5\,\mathrm{\mu Sv\cdot m^{2}/(h\cdot GBq)}\)。
3 实验
3.1 对伽玛辐射功率的测量
对伽玛辐射功率的测量进行于一个平行于放射源放置的轨道上,放射源固定在轨道一端。
测量仪器放置于轨道上的一个托盘。这样可以让仪器处于距离轨道的各种距离上,并且在放射源的一条轴线上的受到照射。
测量结果如表格所示。
| 距离 \(r\) [cm] | \(1/r^2\) | RGD 27091 [\(\mu Sv/h\)] | LB 133 [\(\mu Sv/h\)] | Thermo FH 40G [\(\mu Sv/h\)] |
|---|---|---|---|---|
| 5 | 400 | 1320 | \(0.25\times10^4\) | \(2.1\times10^3\) |
| 10 | 100 | 660 | \(0.1\times10^{4}\) | \(0.84\times10^{3}\) |
| 20 | 25 | 252 | \(0.04\times10^{4}\) | 265 |
| 30 | 11.11 | 133 | \(0.15\times10^{3}\) | 130 |
| 40 | 6.25 | 84 | \(0.1\times10^{3}\) | 80.2 |
| 50 | 4 | 58 | \(0.075\times10^{3}\) | 54.3 |
| 60 | 2.78 | 42 | \(0.45\times10^{2}\) | 34.5 |
| 80 | 1.56 | 27 | \(0.25\times10^{2}\) | 22.2 |
| 100 | 1 | 17 | \(0.18\times10^{2}\) | 17.7 |
| 120 | 0.694 | 12 | \(0.12\times10^{2}\) | 12.2 |
| 150 | 0.444 | 8 | \(0.08\times10^{2}\) | 7.02 |
| 200 | 0.25 | 5 | \(0.04\times10^{2}\) | 3.88 |
| 250 | 0.16 | 3 | \(0.4\times10^{1}\) | 3.4 |
| 300 | 0.111 | 3 | \(0.325\times10^{1}\) | 2.51 |
3.2 对屏蔽特性的测量
为了测量屏蔽特性,一共使用了四种材料。这些材料直接贴着放射源进行屏蔽,然后在材料的另一侧使用仪器对伽玛辐射功率进行测量。
测量结果如表格所示。
| 材料 | RGD 27091 [\(\mu Sv/h\)] | LB 133 [\(\mu Sv/h\)] | Thermo FH 40G [\(\mu Sv/h\)] |
|---|---|---|---|
| 20cm 低密度水泥 | 160 | \(0.21\times10^{3}\) | 178 |
| 20cm 高密度水泥 | 16 | \(0.2\times10^{2}\) | 18.8 |
| 40cm 高密度水泥 | 1.8 | 0.35 | \(200\times10^{-3}\) |
| 5cm 铅 | 11.4 | \(0.15\times10^{2}\) | 14.1 |
4 计算
4.1 放射源的放射活度
4.1.1 绘图表示放射源的辐射功率和距离的关系
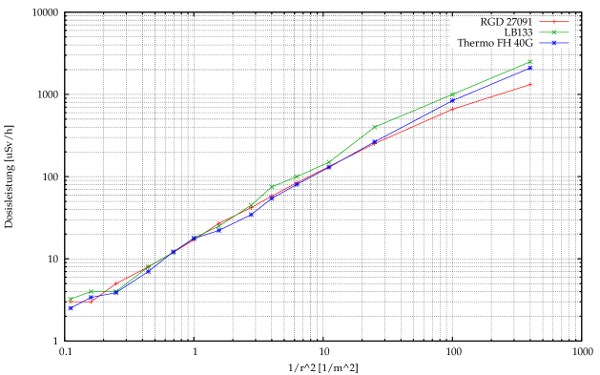
辐射功率和距离的关系如下图。
4.1.2 线性拟合
根据测量结果,可以通过线性拟合的方式,计算放射活度。
我们首先假设式(1)是正确的,也就是说,放射源可以被认为是一个点放射源。 此外还需要考虑自然的本底辐射。这一辐射的效果是,在测量结果中包含大小为\(P_0\)的辐射功率。 对于这种测量的数学模型就是:
\[ P(r)=K\frac{A}{r^{2}}+P_{0} \]
其中,\(K\)是一个给定的常数,\(A\)和\(P_0\)是未知量。
计算的任务就是,根据已知的二维测量结果\( (r_i,P(r_i)) \), 求出未知的\(A\)和\(P_0\)。
注意到,测量仪器相对放射源的距离\(r_i\)是可以相对准确地测量的,而且也和\(P\)不相关, 所以可以利用线性拟合的方式进行计算。 所谓线性拟合的作用是,根据离散的点\( (X_i,Y_i) \),给出下式中\(a\)和\(b\)的值,描述一条形式为
\[ y(x)=a+bx \]
的直线,使得这样一个求和
\[ \sum_i [Y_i-y(X_i)]^2 = \sum_i [Y_i-(a+bX_i)]^2 \]
尽可能的小。为了将本实验的数据借助这种方法进行分析,\(a\),\(b\),\(X_i\)和\(Y_i\)将经由下式进行定义。
\[ a=P_0 \]
\[ b=KA \]
\[ X_i=\frac{1}{r_i^2} \]
\[ Y_i=P(r_i) \]
这种方式对\(b\)和\(a\)给出的解为:
\[ P=\frac{\mathrm{d}D}{\mathrm{d}t}=K\frac{A}{r^{2}} \]
\[ a=\frac{\sum_{i=1}^n X_i^2 \sum_{i=1}^n Y_i - \sum_{i=1}^n X_i \sum_{i=1}^n X_i Y_i }{ n \sum_{i=1}^n X_i^2 - (\sum_{i=1}^n X_i)^2 } \]
为了估计测量的误差,还需要引入一个相关系数\(r_{XY}\):
\[ r_{XY}=\frac{ \sum_{i=1}^n (X_i-\overline{X})(Y_i-\overline{Y}) }{ \sqrt{ \sum_{i=1}^n (X_i - \overline{X})^2 \sum_{i=1}^n(Y_i-\overline{Y})^2} } \]
其中\( \overline{X} \)和\( \overline{Y} \)分别是测量值\(X_i\)和\(Y_i\)的算术平均值。
参数\(b\)的相对误差由下式给出为:
\[ \frac{\delta b}{b}=\sqrt{\frac{r_{XY}^{-2}-1}{n-2}} \]
我们现在将3.1中的14个测量结果代入公式(2)(3)(4),得到下表所列结果。
| 测量仪器 | \(a\) | \(b\) | \(r_{XY}^2\) |
|---|---|---|---|
| LB 133 | 60.5653 | 6.3183 | 0.9742 |
| Thermo FH 40G | 45.1034 | 5.3156 | 0.9781 |
| RGD 27091 | 55.0042 | 3.3503 | 0.9388 |
注意到,在\( x=1/r^2\rightarrow 0\),或者说\( r\rightarrow\infty \)的时候, \(a\)的含义就是自然本底辐射。在实验室中,这个值在大约\( 2\,\mathrm{\mu Sv/h} \) 的级别。所以,上述结果和真实情况的差异很大。 其原因是,在距离放射源比较近的位置,放射源不能被当作点放射源看待。
我们将距离\( r<60\,\mathrm{cm} \)的测量结果丢弃,然后重新进行线性拟合,作为比较,新的结果列表如下:
| 测量仪器 | \(a\) | \(b\) | \(r_{XY}^2\) |
|---|---|---|---|
| LB 133 | 1.1150 | 15.7607 | 0.9978 |
| Thermo FH 40G | 2.2192 | 12.2360 | 0.9770 |
| RGD 27091 | 1.4627 | 15.0420 | 0.9949 |
利用公式(5)可以估计这样计算的相对误差 \(\delta b/b\)。由于\(b=KA\),可以证明\(A\)和\(b\)具有同样的相对误差:
\[ \frac{\delta A}{A}=\frac{K\delta A}{KA}=\frac{\delta(KA)}{KA}=\frac{\delta b}{b} \]
由此求得\(A\)和\(\delta A\)的结果,如下表:
| 测量仪器 | \(a\) | \(b\) | \(r_{XY}^2\) | \(\delta b/b\) | \(A=b/K\)[GBq] | \(\delta A=A\delta b/b\)[GBq] |
|---|---|---|---|---|---|---|
| LB 133 | 1.1150 | 15.7607 | 0.9978 | 0.02712 | 0.1704 | 0.004621 |
| Thermo FH 40G | 2.2192 | 12.2360 | 0.9770 | 0.08910 | 0.1323 | 0.01179 |
| RGD 27091 | 1.4627 | 15.0420 | 0.9949 | 0.04139 | 0.1626 | 0.006730 |
4.1.3 计算结果
测量得到的Cs-137源的放射活度如下。
- 使用LB 133测量:\( (1.7\pm0.0)\times10^{8}\,\mathrm{Bq} \)
- 使用Thermo FH 40G测量:\( (1.32\pm0.12)\times10^{8}\,\mathrm{Bq} \)
- 使用RGD 27091测量:\( (1.63\pm0.07)\times10^{8}\,\mathrm{Bq} \)
理论的放射活度在2.2节已经进行了计算,其结果为:
\[ A_{6.2015}=0.1556\,\mathrm{GBq}=1.556\times10^{8}\,\mathrm{Bq} \]
RGD 27091的结果与这个值是最接近的。
4.2 屏蔽特性
为了评价不同屏蔽材料的性能,需要使用3.2小节的测量数据。
4.2.1 线性衰减系数和误差分析
理论上说,伽玛辐射功率在经历了厚度为\(x\)的材料的屏蔽后,其值可以由下式描述:
\[ P_x=B_D P_{x0} e^{-\mu x} \]
其中:\(B_D\)是剂量增长系数,在本实验中可以近似认为\( B_D \approx 1\); \(P_{x0}\)是测量位置上没有屏蔽时应当具有的辐射功率; \(\mu\)称为线性衰减系数:
\[ \mu=\frac{1}{x}(\mathrm{ln}P_{x0}-\mathrm{ln} P_x) \]
因为对于每种材料和每种测量仪器,对于屏蔽性能的测量只进行了一次,所以这个系数应当直接用(6)式计算出来。
\(\mu\)的不确定度由下式确定:
\[ \varepsilon_{\mu}=\sqrt{ (\frac{\partial\mu}{\partial x}\varepsilon_{x})^{2}+(\frac{\partial\mu}{\partial P_{x0}}\varepsilon_{P_{x0}})^{2}+(\frac{\partial\mu}{\partial P_{x} }\varepsilon_{P_{x}})^{2} }=\frac{1}{x}\sqrt{ \mu^{2}\varepsilon_{x}^{2}+\frac{1}{ P_{x0}^{2} }\varepsilon_{P_{x0}}^{2}+\frac{1}{P_{x}^{2} }\varepsilon_{P_{x} }^{2} } \]
其中,\(\varepsilon_x\),\(\varepsilon_{P_{x0}}\)和\(\varepsilon_{P_x}\)分别是\(x\)、\(P_{x0}\)和\(P_x\)的不确定度。
\(\mu\)具有一个[\(\mathrm{L^{-1} }\)]的量纲,其倒数\(\mu^{-1}\)具有长度的量纲,描述了屏蔽能力。一个有用的定义是半衰厚度:
\[ x_{0.5}=\frac{\mathrm{ln} 2}{\mu} \]
其误差和\(\mu\)的关系是:
\[ \varepsilon_{x_{0.5}}=| \frac{\mathrm{d} x_{0.5} }{\mathrm{d}\mu}\varepsilon_\mu |=\frac{\mathrm{ln} 2}{\mu^2}\varepsilon_{\mu}=\frac{x_{0.5}\varepsilon_\mu}{\mu} \]
如果将\(\mu\)除以物质的密度,就得到了质量衰减系数:
\[ \mu’=\frac{\mu}{\rho} \]
和它的不确定度:
\[ \varepsilon_{\mu’}=\frac{\mu’}{\rho} \]
4.2.2 计算结果
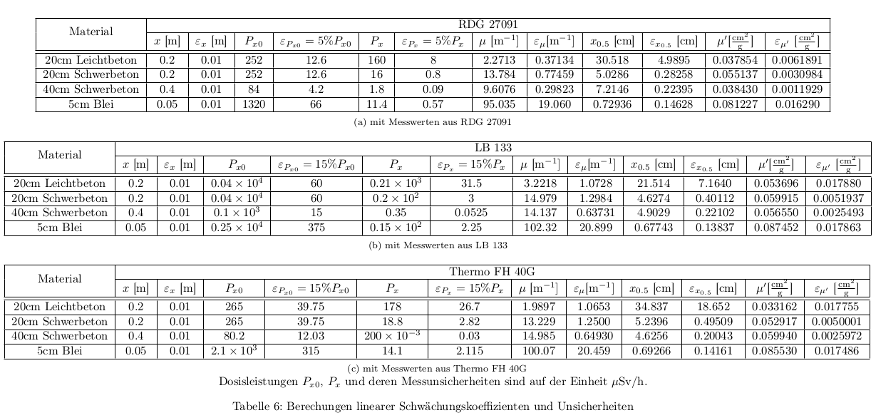
根据(6)到(11)的公式进行计算的结果见附表。其重要的结果在下面的表格中进行汇总:
| 物理量 | 材料 | RDG 27091 | LB 133 | Thermo FH 40G |
|---|---|---|---|---|
| \(\mu\) [\(\mathrm{m^{-1} }\)] | 20cm 低密度水泥 | \(2.27\pm0.37\) | \(3.2\pm1.1\) | \(1.99\pm1.06\) |
| 20cm 高密度水泥 | \( (1.38\pm0.08)\times10^{1} \) | \((1.5\pm0.1)\times10^{1}\) | \((1.32\pm0.1)\times10^{1}\) | |
| 40cm 高密度水泥 | \(9.61\pm0.30\) | \((1.4\pm0.0)\times10^{1}\) | \((1.50\pm0.06)\times10^{1}\) | |
| 5cm 铅 | \((9.50\pm1.91)\times10^{1}\) | \((1.0\pm0.2)\times10^{2}\) | \((1.00\pm0.20)\times10^{2}\) | |
| \(x_{0.5}\) [cm] | 20cm 低密度水泥 | \((3.05\pm0.50)\times10^{1}\) | \((2.1\pm0.7)\times10^{1}\) | \((3.48\pm1.86)\times10^{1}\) |
| 20cm 高密度水泥 | \(5.03\pm0.28\) | \(4.6\pm0.4\) | \(5.24\pm0.50\) | |
| 40cm 高密度水泥 | \(7.21\pm0.22\) | \(4.9\pm0.2\) | \(4.62\pm0.20\) | |
| 5cm 铅 | \((7.29\pm1.46)\times10^{-1}\) | \((6.8\pm1.4)\times10^{-1}\) | \((6.93\pm1.42)\times10^{-1}\) | |
| \(\mu’\) [\(\mathrm{cm^2/g}\)] | 20cm 低密度水泥 | \((3.78\pm0.62)\times10^{-2}\) | \((5.4\pm1.7)\times10^{-2}\) | \((3.32\pm1.78)\times10^{-2}\) |
| 20cm 高密度水泥 | \((5.51\pm0.31)\times10^{-2}\) | \((6.0\pm0.5)\times10^{-2}\) | \((5.29\pm0.50)\times10^{-2}\) | |
| 40cm 高密度水泥 | \((3.84\pm0.12)\times10^{-2}\) | \((5.6\pm0.2)\times10^{-2}\) | \((5.99\pm0.26)\times10^{-2}\) | |
| 5cm 铅 | \((8.12\pm1.63)\times10^{-2}\) | \((8.7\pm1.8)\times10^{-2}\) | \((8.55\pm1.75)\times10^{-2}\) |
由这一结果可以得到如下结论:
- 对20cm厚的高密度水泥,和对40cm厚的高密度水泥的测量结果给出相似的\(\mu\)、\(x_{0.5}\)和\(\mu’\)结果。 因此可以说,这三个量体现了材料的本身特性,和几何尺寸无关。
- 与高密度水泥相比,低密度水泥的屏蔽能力明显较弱。
- 铅的线性衰减系数远超水泥,其质量衰减系数也非常高。 这意味着,在需要同样的防护能力时,用铅防护可以将防护措施的几何体积大大缩小,见4.2.3小节的计算。 因此,铅是十分适合作为辐射防护的材料。
4.2.3 以铅板为例计算其屏蔽的厚度
现在我们计算,对于伽玛辐射功率为\(10\,\mathrm{mSv/h}\)的辐射源,使用铅板进行防护所需要的厚度。 目标是,在0.5m的距离上,将辐射功率降低到\(25\,\mathrm{\mu Sv/h}\)的水平。
对于铅来说,\(\mu\)的平均值由前面的实验确定:
\[ \mu_{\mathrm{Blei}}=\frac{1}{3}(95+100+100)=98.3\,\mathrm{m^{-1}} \]
所需要的厚度\(d_{\mathrm{Blei}}\)为:
\[ d_{ \mathrm{Blei} }=\frac{1}{ \mu_\mathrm{Blei} } (\mathrm{ln} D_0 - \mathrm{ln} D)= \frac{1}{98.3} (\mathrm{ln} 10000- \mathrm{ln} 25) \, \mathrm{m} = 6.1\,\mathrm{cm} \]
这个厚度只是整个设计距离的12%。在实验中,这样的防护,使用铅砖来实现即可。
附表(德语报告第7页)