1 概要
《校准控制棒》的核反应堆实习于2015年6月2日在德累斯顿工业大学的AKR-2反应堆装置进行。 实验内容有,借助测量稳定的反应堆周期和INHOUR公式的方法,确定3根控制棒中的2根的控制棒特性曲线。 此外,根据测量结果,导出反应堆的总、预留和停堆反应性。
2 基础知识
控制棒是核反应堆中重要的装置。其作用是控制反应堆的反应性\(\rho\)。根据反应性的定义
\[ \rho = 1-\frac{1}{k} \]
这样影响到的是反应堆增殖系数\(k\),其决定了反应堆功率的增长趋势。
在反应堆中,控制棒是一个活动的零件。它可以插进反应堆,或者从反应堆中被拔出。 在反应堆中,控制棒会吸收中子。这样链式反应就会因为\(k\)的下降而被减缓甚至停止。 如果控制棒被完全抽出,则会相反导致\(k>1\),进而功率上升。 控制棒的位置唯一决定了反应性。这个相关的关系就是控制棒的特性曲线。
在本实习中其实测量的是反应堆倍周期\(T_2\)。在知道了\(T_2\)之后, 可以通过对其乘以一个系数获得反应堆周期:\(T_s = T_2 / \mathrm{ln} 2 = 1.443 T_2\)。 利用INHOUR公式:
\[ \rho \approx \frac{1}{T_s} \sum _{i=1} ^6 \frac{\beta_i}{\lambda_i} \]
或者,习惯上也写成相对于\(\beta\)(所有新产生的中子中的缓发中子比例)的形式:
\[ \rho’ = \frac{\rho}{\beta} = \frac{1}{T_s} \sum _{i=1} ^6 \frac{\beta_i}{\beta} \frac{1}{\lambda_i} = \frac{1}{T_s} \sum _{i=1} ^6 \frac{\alpha_i}{\lambda_i} \]
其中\(\alpha_i = \beta_i / \beta\),是和\(\lambda_i\) (\(i=1,2,3,…,6\))一起给出的常数, 可以得到用\(\rho\)或者\(\rho’\)写出的反应性结果。 根据下文所叙述的实验过程,可以看出,这些反应性只是由被校准的控制棒的各部分的面积所分别贡献。 换句话说,实际上测量到的是反应性的变化量\( \Delta \rho / \Delta z \)。 \(\Delta\rho/\Delta z\)相对于\(z\)的关系,其中\(\rho\)是反应性,\(z\)是控制棒的位置,被称为微分形式的控制棒特性曲线。 其积分之后的形式,就是积分形式的控制棒特性曲线。
控制棒影响的是反应堆的反应性变化。控制棒对反应性的全部影响能力,就是总反应性。 此外,我们知道,控制棒在某个位置组合的时候,反应堆就会临界。此时如果继续拔出控制棒,就会导致反应堆超临界。 反应堆从临界到超临界的最大可能的反应性的差别,就是预留反应性。 这是将控制棒从临界时的情况到全部抽出反应堆所造成的两种情况的反应性差别。 反过来,当全部控制棒从临界的情况完全插入反应堆,就应当造成停堆。这时控制棒从临界情况削减的反应性,就是停堆反应性。
3 实验过程

- 在实验前,一根控制棒(记作控制棒3)被从反应堆中完全抽出。 另一根控制棒(记作控制棒1)完全留在堆内。 第三根控制棒(记作控制棒2),被用作保持反应堆临界条件。
- 首先将反应堆维持在一个较低的功率水平临界,例如\(P_0 \approx 0.5 \mathrm{W}\)。 这种条件的选取,需要务必留下一个较大的功率上升空间,因为在稍后的测量过程中, 将会在一段相对很长的时间上经历超临界过程和功率上升。
- 反应堆临界后,控制棒1被抽出一个距离 \(\Delta z_{1.1}\) 。 因此反应堆会超临界。 测量从此刻开始,直到反应堆功率翻倍(\(P=2P_0\))的时间,这就是反应堆倍周期\(T_{2.1}\)。
- 之后将控制棒3插入反应堆。这将导致反应堆的功率上升停止。 继续插入控制棒可以降低反应堆的功率,以便将其功率重新降低到\(P_0\)。 之后继续调整控制棒3的位置,使得反应堆重新临界。 在这个过程中,控制棒3产生了\(\Delta z_{3.1}\)的位移,以便抵消控制棒1导致的反应性变化。
- 已知了反应堆倍周期\(T_{2.1}\)之后,可以根据INHOUR公式求出反应性的变化\(\Delta \rho_1\)。 这部分的反应性可以通过将控制棒1抽出\(\Delta z_{1.1}\)产生, 也可以通过在结束状态下将控制棒3进行\(-\Delta z_{3.1}\)的位移,即虚拟的抽出过程产生。
- 重复以上过程,直到控制棒1被完全抽出反应堆,亦即控制棒3完全插入反应堆。
用这样的方法,每根控制棒的行程高度都会被分成很多小段:控制棒1是 \(\Delta z_{1.1}\), \(\Delta z_{1.2}\), \(\Delta z_{1.3}\),… \(\Delta z_{1.n}\), 控制棒3是 \(\Delta z_{3.1}\), \(\Delta z_{3.2}\), \(\Delta z_{3.3}\),… \(\Delta z_{3.n}\)。 并对应求出单独每个这样的分段可导致的反应性变化 \(\Delta \rho_1\), \(\Delta \rho_2\), \(\Delta \rho_3\),… \(\Delta \rho_n\)。
4 对测量结果的计算
4.1 反应性的增量
完整的测量值在后文。 最重要的值(控制棒位置,由\(z_1\)和\(z_3\)表示,其单位用u表示,以及平均反应堆倍周期\(\overline{T_2}\)), 以及由之算出的结果(\(T_s\)、\(\rho’\)和\(\frac{\Delta \rho’}{\Delta z_i}\)),在表格中进行展示。 (注释:表格中kritisch表示临界,Messwerte表示测量结果,Berechnungen表示计算结果)。
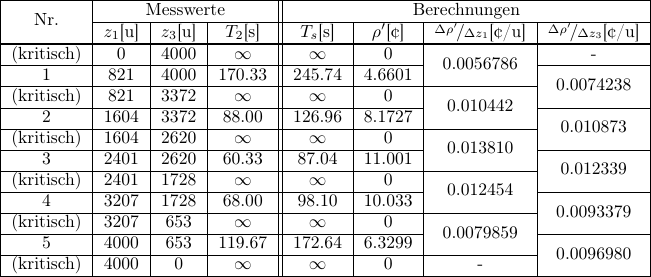
对于控制棒1,计算\(\frac{\Delta \rho’}{\Delta z_1}\)是从上向下进行的, 亦即使用成对的、具有共同的\(z_3\)的测量值。 相反,对于控制棒3,\(\frac{\Delta \rho’}{\Delta z_3}\)是从下向上进行的, 亦即使用了\(z_1\)相同时的值。这是因为对于控制棒3我们的计算基于一个设想的、和插入反向的拔出过程。 这一区别通过表格右两列的单元格排布来表示。
4.2 微分和积分形式的控制棒特性曲线
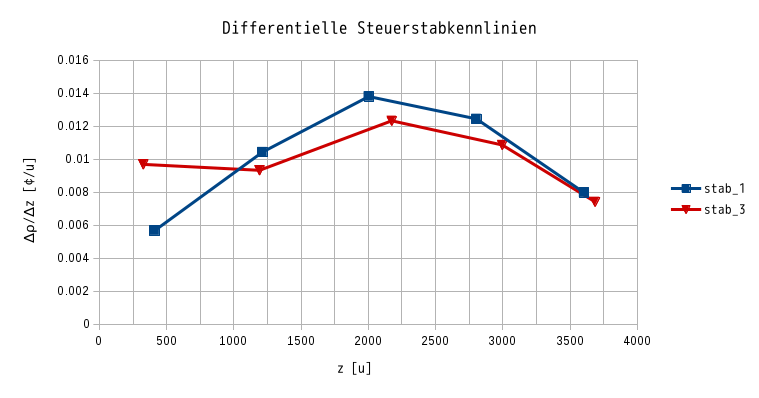
根据如上计算,我们可以用曲线表示控制棒的微分形式的特性曲线。 然而要注意的是,结果在X轴(控制棒位置\(z\))上放置于哪个坐标。 控制棒的插入和拔出是一个相对缓慢的、持续几十秒的过程,但控制棒的位置只要变化,反应性就会发生变化。 在本实验报告中,将对于所有的结果,取用控制棒位移的中间值。
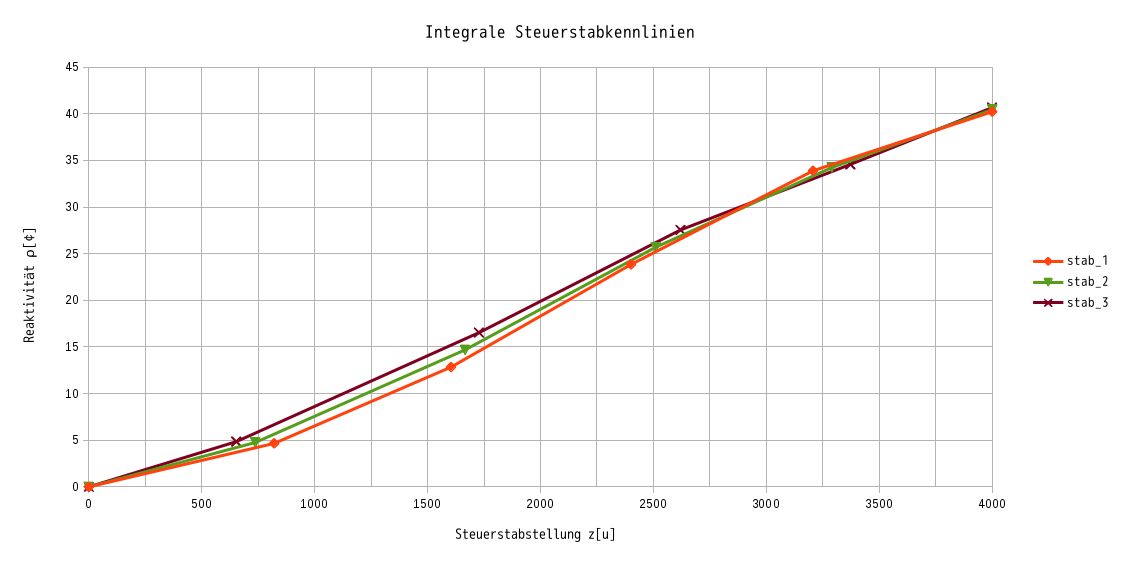
积分形式的控制棒特性曲线,可以通过对所有的\(\frac{\Delta \rho}{\Delta z}\)对\(z\)求和得出,如图。 需要注意的是对于控制棒2的特性曲线。控制棒2由于和控制棒1、3有相似的物理构造,其特性曲线被假定是两条测出曲线的平均值。 这个假定使得计算反应堆的总、预留和停堆反应性所需的数据得以满足。
4.3 总、预留和停堆反应性
利用积分形式的控制棒特性曲线,可以直接根据控制棒的位置读出对应的反应性。
总反应性是对应于整个控制棒高度的反应性:
\[ \rho’_{\mathrm{1,总}} = 40.217\,¢ \]
\[ \rho’_{\mathrm{2,总}} = 40.436\,¢ \]
\[ \rho’_{\mathrm{3,总}} = 40.656\,¢ \]
将以上三式求和就得到了总计的可用反应性:
\[ \rho’_\mathrm{总} = \sum _{i=1} ^3 \rho’_\mathrm{i,总} = 121.309\,¢ \]
预留反应性和停堆反应性是从临界状况下出发计算的。首先需要了解在不同的临界状况时3根控制棒的位置组合,见表格。之后,两个反应性的定义是:
\[ \rho’_\mathrm{预留} = \rho’_\mathrm{总} - \rho’_\mathrm{停堆} \]
\[ \rho’_\mathrm{停堆} = \sum _i \rho’_i(z_i) \]
| Nr. | \(z_1\)[u] | \(z_2\)[u] | \(z_3\)[u] | \(\rho_1’(z_1)\)[¢] | \(\rho_2’(z_2)\)[¢] | \(\rho_3’(z_3)\)[¢] | \(\rho’_\mathrm{预留}\)[¢] | \(\rho’_\mathrm{停堆} \)[¢] |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 3139 | 3996 | 0.000 | 32.776 | 40.604 | 47.928 | 73.380 |
| 2 | 821 | 3139 | 3372 | 4.662 | 33.776 | 34.565 | 49.304 | 72.004 |
| 3 | 1604 | 3141 | 2620 | 12.839 | 32.796 | 27.543 | 48.130 | 73.178 |
| 4 | 2401 | 3141 | 1728 | 23.846 | 32.796 | 16.536 | 48.130 | 73.178 |
| 5 | 3207 | 3141 | 653 | 33.884 | 32.796 | 4.848 | 49.780 | 71.528 |
| 6 | 4000 | 3141 | 0 | 40.217 | 32.796 | 0.000 | 48.295 | 73.013 |
也就是说,AKR-2反应堆在3根控制棒全部抽出的时候,有将预留反应性控制在\(49.780\,¢\)的能力。 当3根控制棒全部插入的时候,可以至少在堆内造成\(71.528\,¢\)的停堆反应性。
5 附录
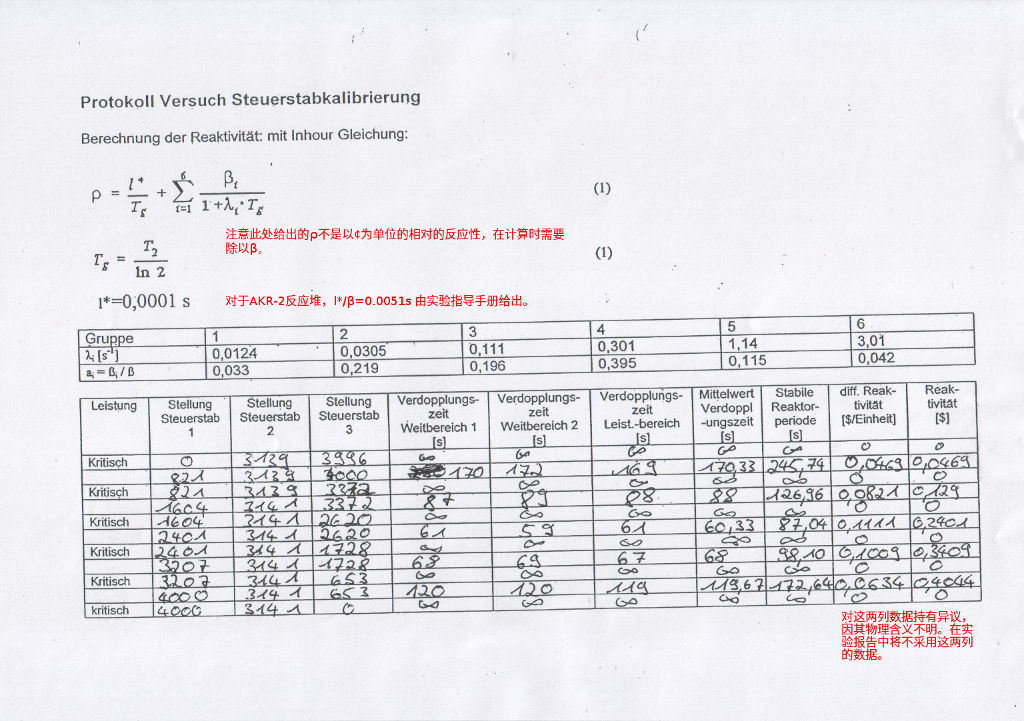
实验的原始数据,和用来计算反应性的INHOUR公式(未经约化)、常数及其说明,见下图扫描件。