目录
1. 前言
NeoAtlantis应用科学和神秘学实验室根据一次神秘学研究,得知使用磁铁构成的莫比乌斯环可能具有 某些特殊的力学特性[*]。 根据提示,这种莫比乌斯环可以使用强力的永久磁铁构成,其中两个环分别安装在轮状的支撑结构上。 现在试图研究其中一个环对另一个环施加的力,尤其是对轮轴的力矩。
[*] 关于这一点,本文不会详细描述,如果您看完本文有何猜想,或者想进一步了解,请和作者联系。
2. 研究方法
2.1 莫比乌斯环的数学模型
将一张纸条的一端扭转180度,然后与纸条的另一端粘贴在一起,可以构成一个莫比乌斯环。 这样的莫比乌斯环只有一个平面,也只有一条边。
但作为数学模型,有一种更为“干净”的办法定义:考虑在 X-Y 平面上有一条半径 R,它绕着轴 Z 旋转(蓝色)。 在半径R的另一端有一条线段 r(红色),位于 R 和 Z 轴所构成的平面内,并绕 R 的端点旋转,其转速,是R的一半。
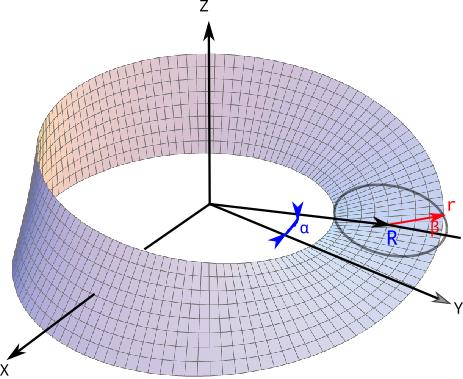
这样,α的角度(R所旋转的角度)就始终是β(r所旋转的角度)的二倍。 R旋转一周360度,r旋转180度,返回初始位置,就构成了一个莫比乌斯环。
数学描述上,首先是Z的坐标:
\[ Z = R + r \textrm{sin}(\beta) = R + r \textrm{sin}(\frac{1}{2}\alpha) \]
X 和 Y 的坐标,可以由 R 与 r在XY平面上的投影 两部分之和分解得到:
\[ X = [R + r \textrm{cos}(\beta)]\textrm{cos}(\alpha) = [R + r \textrm{cos}(\frac{1}{2}\alpha)]\textrm{cos}(\alpha) \] \[ Y = [R + r \textrm{cos}(\beta)]\textrm{sin}(\alpha) = [R + r \textrm{cos}(\frac{1}{2}\alpha)]\textrm{sin}(\alpha) \]
2.2 磁铁相互作用的模型
空间中两个磁铁的相互作用力很复杂,关于这个话题有一个专门的维基百科进行介绍。
本研究中使用吉尔伯特模型简化磁铁的磁感线。这种模型假设磁铁由成对的“磁单极子”构成,类似电荷那样,有N和S两种。 因为使用了点状的简化模型,在工程计算上比较方便,其磁感线也很接近实际情况(至少在磁铁外面是这样的)。

(上图:安培电流模型,下图:吉尔伯特磁荷模型)
为了简化计算,我们忽略公式中的常数,假设两个磁荷的相互作用力遵从平方反比定律:
\[ F = \frac{q_1q_2}{r^2} \]
当\(q_1\)和\(q_2\)为同号时,相互排斥,反之相互吸引。
3 编程计算
3.1 安装了磁铁的莫比乌斯环
我们使用如下假设生成一个安装了磁铁的莫比乌斯环:
- 环的几何形状由上一章的公式指定
- 我们在一个圆周360度内,选取N=24个角度,将圆周均分,并根据公式得出莫比乌斯环的一个端点
- 在上述模型中,将 r 反向(180度),可以得到莫比乌斯环在每个截面上的另一个端点
- 这样的两个端点,分别是磁铁的N和S极,具有磁荷1和-1
计算中,假设两个莫比乌斯环的基础半径 R=25cm,磁铁长度 2r=10cm,其中左侧环位于(0,0,0)点,右侧环位于(0.7,0,0)点,即在右侧70cm处。
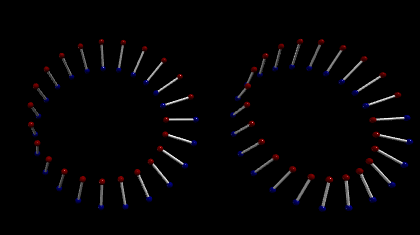
使用 VPython,可以根据如上描述展示这样构成的两个圆环(红色为N磁荷,蓝色为S磁荷)。
3.2 莫比乌斯环之间的相互作用力
我们假设左侧的莫比乌斯环固定不动,现在需要研究它对右侧圆环的作用力。
为了研究作用力,我们将右侧圆环从0度旋转360度,然后将左侧圆环中的48个磁荷与右侧圆环中的48个磁荷分别进行相互作用计算,得到48x48个作用力。
将这些作用力对右侧圆环的圆心求出力矩,提取在Z轴上的分量,求和,得到合力矩。对这一力矩积分,就可以得到右侧圆环旋转一周受左侧环中磁铁影响所接受的功。
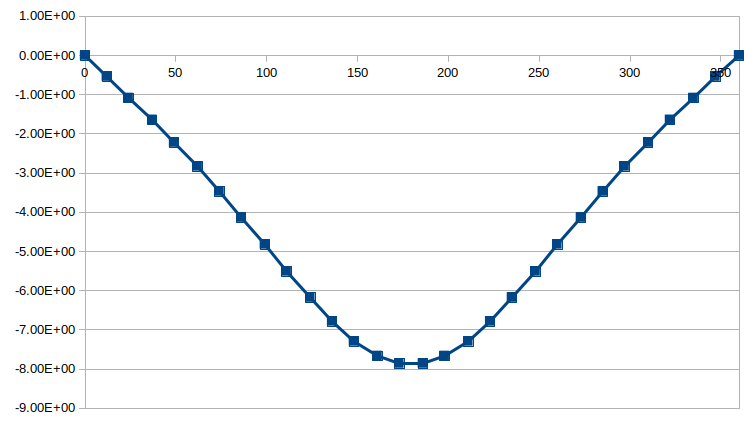
注意到,即使左侧莫比乌斯环不动,右侧环旋转一圈所受到的力矩,总是具有相同的符号,并且旋转一周所得积分不为零。 因此,这是否是真实情况下可以实现的结果,有待进一步研究。 然而需要指出,虽然磁铁的吉尔伯特模型有诸多不足——因为自然界实际上不存在磁单极子——但如果将上述结果应用于电荷,则是没有模型问题的。如果计算没有出现错误,这意味着什么呢?
附录 - 计算程序
本文所用的计算程序包括两个文件:simplified_magnet.py 和 model.py,运行后者可以开始计算。
simplified_magnet.py
#!/usr/bin/env python3
#from vpython import * # 如果想用下面class的visualize()方法,请启用
from math import *
from numpy import linspace, array
class SimpleMagnetMobiusStrip:
def __init__(self, center, radius, magnetRadius, offsetAngle=0, strength=1, rightHand=False):
self.center = center
self.centerX, self.centerY, self.centerZ = center
self.radius = radius
self.magnetRadius = magnetRadius
self.offsetAngle = offsetAngle
self.strength = 1
self.rightHand = rightHand
def __iter__(self):
N = 24
for angle in linspace(0, 2*pi, N):
theta = (angle + self.offsetAngle) / 2.0
if self.rightHand: theta = -theta
z1 = self.centerZ + sin(theta) * self.magnetRadius
z2 = self.centerZ - sin(theta) * self.magnetRadius
deltaR = cos(theta) * self.magnetRadius
R1 = self.radius + deltaR
R2 = self.radius - deltaR
x1 = self.centerX + cos(angle) * R1
y1 = self.centerY + sin(angle) * R1
x2 = self.centerX + cos(angle) * R2
y2 = self.centerY + sin(angle) * R2
yield (
array([x1, y1, z1, self.strength]),
array([x2, y2, z2, -self.strength])
)
def visualize(self):
iterator = self.__iter__()
a0, b0 = None, None
for a1, b1 in iterator:
sphere(pos=vector(*a1[:3]), radius=0.01, color=vector(0.5, 0, 0))
sphere(pos=vector(*b1[:3]), radius=0.01, color=vector(0, 0, 0.5))
curve(vector(*a1[:3]), vector(*b1[:3]))model.py
#!/usr/bin/env python3
from math import pi
from simplified_magnet import *
from numpy.linalg import norm
from numpy import cross, array
s1 = SimpleMagnetMobiusStrip(
center=array([0, 0, 0]),
radius = 0.25,
magnetRadius=0.05,
offsetAngle=0,
strength=1
)
def force(point1, point2, s1, s2):
d = norm(point1-point2)
return s1 * s2 * (point2-point1) / (d**3)
def momentum(force, forcePoint, center):
r = forcePoint - center
return cross(r, force)
c = 0
intMZ = 0
N = 30
for offset in linspace(0, 2*pi, N):
s2 = SimpleMagnetMobiusStrip(
center=array([0.7, 0, 0]),
radius = 0.25,
magnetRadius=0.05,
offsetAngle=offset,
strength=1
)
M = array([0.0, 0.0, 0.0])
for a1, b1 in s1:
for a2, b2 in s2:
f1 = force(a1[:3], a2[:3], a1[3], a2[3])
f2 = force(a1[:3], b2[:3], a1[3], b2[3])
f3 = force(b1[:3], a2[:3], b1[3], a2[3])
f4 = force(b1[:3], b2[:3], b1[3], b2[3])
m1 = momentum(f1, a2[:3], s2.center)
m2 = momentum(f2, b2[:3], s2.center)
m3 = momentum(f3, a2[:3], s2.center)
m4 = momentum(f4, b2[:3], s2.center)
M += sum([m1, m2, m3, m4])
intMZ += M[2] * (2 * pi / N)
print("%3d" % (offset / pi * 180.0), " ", "%E" % M[2])
print(intMZ)