本文所谓JPEG图片加密，不是指将图片的二进制数据加密。 加密二进制数据的方法有很多，可以做到十分安全，但缺陷就在于，加密后的文件不再是图片了。 这就限制了这类算法在只能传送图像的场合（例如互联网上的图片附件，或者某些音视频媒体）中的运用。

本文进行的实验，与此不同，是关于一种将JPEG图片打乱并进行变换的算法， 加密后的图片仍然保持为JPEG图像格式，可以和普通的JPEG图像一样传送。 甚至，加密的图片也可以被重新压缩降低画质，这样解密后的图像仍然能（在低画质下）查看。

1. 原理

1.1 图像背后是数据

我们每天在互联网上都看到各种图片，用手机也可以很方便的拍摄。拍摄的图像，在各类电子设备中，是怎么处理的呢？

读者大概知道，图像是以文件的形式存储的，图像文件可以用各种软件打开，展示在屏幕上，或者用打印机打印。 无论哪种展示方式，图像最后都会在一个矩形的点阵上（比如屏幕），以各个点颜色的亮暗或者深浅，来呈现出来。

但是，文件——也就是指导软件产生这样的点阵的数据——存储的是什么呢？

这个问题就比较复杂了。

如果读者用过Windows的画图软件（mspaint.exe），应该了解一种基础的BMP格式。

BMP就是很直觉地将每个点阵的值直接用计算机内的字节表示。 一幅100x200像素的图片，每个像素用RGB方式表示颜色， 每个颜色（红R，绿G，蓝B）有0到255，一共256（2的8次方）种取值，计算机中每个字节也能表示0到255， 这样一个像素就占据3个字节。一共有20000个像素，就需要60000字节，大约60kB不到。

很多时候图像的颜色虽然多彩，但色彩的种类其实并不多，比如各种科学图像，虽然是彩色的，但色彩种类少于256种，有的可能只有几十种。 这样就没必要为每个像素记录RGB三色的配方，只要记录每个像素使用的颜色在“调色板”上的位置即可。 这就是GIF图片。（GIF图片除了使用了索引之外，还使用了一种无损压缩算法，将重复的数据放到一起，更加减少尺寸）。

还有一种更加复杂的技术，也是当今互联网上仍然比较流行的，就是JPEG图片。 JPEG图片和以上图片格式都不一样：它不直接记录图片的色彩信息，而是如何重现这些信息的另外一种信息。

1.2 JPEG图片格式

我们首先说明，JPEG是一种将图片进行有损压缩的存储格式。 有损的意思，就是说图片在经过处理后， 虽然看上去仍然保持了大致的内容，但细节上会有所损失。 以这种代价换来的，是图片的数据量明显减少，便于在互联网上传播。

举个例子，如果读者用手机拍摄了一张照片，然后将它用JPEG格式存储到网络相册， 那么之后读者看到的图片，一定是和原图有所差异的。

JPEG图片处理数据，进行压缩的核心思路，是将空间域的数据（也就是展示给我们看的三色明暗数据在空间—-亦即二维的屏幕或者纸张—上的分布）， 首先通过二维的离散余弦变换（DCT变换），变成频域数据。

频域数据体现的是图像在各个尺度上的细节变化：如果一个范围内的图像只是纯色，那么这个范围内图像的“频率”就很低。 如果在同样这个范围上我们拍摄一缕头发，那么很细的头发在数学上看就是“高频”的信息。

JPEG压缩的方式，就是根据需要，略去一定程度的高频信息，然后再用改进的编码方式将数据用尽可能短的方式表示出来。 想象一张人物摄影：观感上对我们重要的信息，是人的轮廓、发型、五官、衣服的颜色，但每一根头发和睫毛的细节，就不那么重要。 JPEG压缩算法，就是利用了人的这个特点，将细节信息按照一定的程度省略，将图片的数据减少。

关于DCT变换，我们用下图这只狒狒举个例子。

左图的红色通道经过DCT变换之后的结果，放到右边的图上显示出来。

DCT变换是在8x8像素的块上进行操作的，所以左图尺寸256x256像素，计算之后就成了右图的32x32个矩阵。 每个矩阵的值按照比例涂色显示出来。

每个DCT矩阵中，左上角的一个系数一般是最大的，这就是右图中比较明显的亮点。 这个系数称作DC系数，是整个8x8像素块的平均值。 矩阵的其他参数（称为AC参数），就是用不同频率“测量”这个像素块得到的强度。

我们首先看左边的原图。这个图像的特点是什么呢？ 狒狒的毛发是很复杂的，属于高频成份较多，而鼻子附近的颜色就比较平滑，低频部分较多。

将这个图（的红色通道）通过DCT变换放到右侧，就可以很亮（值很大）的低频区域的DC系数。

2. 如何加密JPEG图像

加密的目的，是希望被加密的东西只能在有一个密钥的情况下才可以被解开。 放到图像上，我们就是希望，这个图像在没有密钥的人那里不能展示出应有的信息。

有很多手段可以做到这一点。 比如我们可以将图像文件当作任意的数据文件，那么常见的数据加密算法，比如AES，就可以直接应用在上面。

但这样做有个缺点：加密的结果，就是一个普通的数据文件，无法作为图像打开，也无法像其他图像进行展示。

本文的目标，则是寻找另一种加密方式，要求加密JPEG图像，且加密后的结果仍然是一个JPEG图像。

2.1 拼图化

最简单的思路，就是将JPEG打乱成拼图。

我们注意到JPEG的图像是以8x8的像素块作为单位进行操作的。像素块之间没有联系。 所以如果我们能将JPEG图像的像素块打乱顺序，而将打乱和恢复的过程用密码算法控制， 那么在没有密钥的情况下，将加密后的图片恢复出来，就需要了解各个像素块之间的联系，这是即便可能也不容易的任务。

我们用下图作为例子:

打乱后的效果是这样：

那么，如何制造一种用密码算法控制的打乱与恢复过程呢？

这个问题其实不难，我们一步一步来。

第一步是如何用一个随机的序列打乱像素块。如果我们为像素块编号，从 1 到 N ：

• 那么原始的图像，就是一个1, 2, 3, 4, …, N的顺序排列。
• 而打乱之后，就是一个按照将1, 2, 3, 4, …, N这些元素随机乱序排列得到的图像。

加密的过程，就是制造一个乱序排列，然后将顺序的结果与之对应，转移图像的数据，重新拼出乱序图像的过程。

解密的过程，就是重新算出应有的乱序排列，然后将图像中相应位置的块，移动到正确（顺序位置）的过程。

第二步是如何生成这样的一个包含从 1 到 N ，无重复元素的乱序排列的过程。

这个过程是一个经典的教科书内容。我们可以采用Fisher-Yates算法, 用伪代码描述起来很简单：

function randperm(n)
  P = [1:n]                         // 生成一个顺序排列的P，从1到n
  for i = n downto 1                // 由 i=n 循环到 i=1
    z = random(i)                   // 获取一个均匀分布的随机数 z，其大小在 1 到 i 之间（包含端点）
    swap(P(i),P(z))                 // 将 P 排列中位于位置 i 和 z 的两个值对调
  end
return P

第三步就是如何控制第二步的关键，random函数的输出了。 这一步有很多解决方法，要点是将random函数的输出和用户的密钥绑定起来，制造一个伪随机数发生器（PRNG）。 我们可以用某些密码学上的哈希函数，比如SHA512，来做到这一点。 比如将密钥用哈希函数处理，得到的伪随机字节每4个一组，就可以得到一系列32比特的随机数字。 如果随机数字的个数不够，可以将密钥和一个计数器放在一起输入哈希函数：SHA512(key+'0001'), SHA512(key+'0002')…

2.2 提高安全性

2.1所述拼图算法有一个问题：每个拼图的碎片，都是原图的一部分。

这样和拼图游戏一样，仍然可以借助计算机，将邻近的拼图碎片寻找出来，进而恢复原图。

所以我们提高加密质量所面临的一个问题就是，能否将图像进行这样的变换，使得

1. 这个变换对于JPEG压缩仍然是稳定的：对压缩后的图像进行逆变换，仍然可以得到有意义的图像；
2. 这个变换的结果，可以改变图像的内容（！！！），使得根据碎片的内容来拼回原图不再可能。

3 通过置乱DCT变换矩阵的元素进行加密

上面提到的两个提高加密质量的措施能否实现呢？ 我们的答案是肯定的。

我们说，为了保证图像在压缩后也能成功解密，那么我们就要寻找一种对压缩过程稳定的算法。

JPEG的压缩过程，除去所有的无损压缩步骤，造成数据损失的地方只有一处：量化(Quantization)。

3.1 观察量化过程

量化过程，就是将8x8像素矩阵DCT变换后，将结果中的每个元素分别用一个对应的量化矩阵中相应位置的数字去除的过程。 除掉的数字取整，就是最后的结果。

Wikipedia上有对此的一段例子，这里直接搬运过来。下面是一个DCT变换的结果：

一个典型的量化矩阵的系数如下：

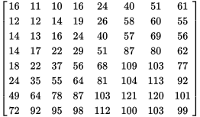
那么量化的结果如下：

请读者仔细观察第二个矩阵（量化矩阵的系数）。 矩阵右下角的数字比左上角的大，这样在进行除法时对高频部分的缩小，就要比左上角的低频部分多一些。 这样导致的量化结果，就是矩阵右下方多出很多个0，0在最后的压缩编码中是基本会被省略掉的，这样就节约了需要记录的数据量。

这个量化矩阵对于一个指定压缩比的JPEG文件是常数。 这样我们得出另一个观察：该过程对DCT矩阵中相对位置相同的元素是线性的。

假设一个DCT矩阵第二行第三列的数字是X， 将这个数字和第二个DCT矩阵的第二行第三列数字Y交换，则X和Y在被压缩时都仍然会被14除（以上图为例）， 在解码时也都被乘以14。这样虽然两个DCT矩阵画出的像素点阵是不同的了，但它们都携带了互相的信息。 在改变压缩率的同时，X和Y都会被按照相同的倍率放大或者缩小，而不影响其他的参数。

3.2 举个例子验证思路

下面我们准备用Lenna图验证上面的思路。

计划是找一张512x512像素的灰度图，然后得到行列各64块（512/8=64）像素碎片。 我们直接将第一行第一个碎片的DCT矩阵的左上角4个系数，与最后一行最后一个矩阵中相应位置的系数交换， 让第一行第二个和最后一行倒数第二个交换……如此类推，如图：

这样我们就得到了一幅很有趣的图，请和原图对比：

仔细观察这两幅图：

• 注意看这幅“杂交”过的图中Lena人像的轮廓，尤其是右部肩膀部分和上部的帽檐。 这些部分属于未经搬运的高频系数所产生，故依然保留。
• 因为我们交换了左侧和右侧的低频系数，所以整体图形看起来被扭转了180度。
• 注意Lena的头发和帽子上的装饰部分，因为其所携带的低频被移到右上方， 所以已经看不出明显的轮廓。
• 注意新图背景右侧的建筑，其轮廓和原图不同: 我们生成了新的图像。

3.3 真正的加密

现在可以猜测，相较于之前的打乱图像8x8碎片的做法（可以看作是打乱DCT整个8x8系数矩阵的特例）， 我们可以在更深的层次上，打乱整个图像的DCT矩阵。

最极端的一种做法是对矩阵中的64个元素在整个图像范围中全部重排， 比如对矩阵DCT1，第一行第一个元素和DCT5的对应元素互换， DCT1的第一行第8个元素，和DCT302的对应元素互换……但这种做法消耗的计算量可能很大。

或者我们将矩阵分成4个4x4的子矩阵：左上，左下，右上，右下，然后对这个4个部分分别重排， 这样就会快很多。

用Lenna图实验，加密后的图像，并再度解密，是这样的：

值得一提的是，这里的加密除了交换DCT矩阵的子矩阵之外，并没有调换碎片的位置。 由于我们对4个子矩阵进行了重排，所以在加密后的图中已经看不到了原图的痕迹（类似3.2例中的“水纹”）。

然后我们将加密后的图压缩，使用GIMP打开，然后重新导出成JPEG格式，质量选择5%， 这样可以看到拼图碎片变得平滑(几乎成了纯色块)，细节丢失，文件大小从原来的30多kB降到了不到5kB。

然后解密：

可以看到解密后的图像仍然具有很好的可读性(和正常被剧烈压缩过的JPEG图像一样)。

4 其他一些絮叨

本文的验证过程， 证明通过置乱DCT变换矩阵的子矩阵来进行加密是有效的方式，可以保证图像在经过压缩之后仍然保持可以解密。

由于缺乏相应的代码库，只能使用GNU Octave来验证，并没有写出可以应用的代码。

但是考虑到JPEG图像的二进制数据，可以通过HTML5中的data-uri方式简单地获取， 可能我们只需要一个简单的库，能解码JPEG的文件格式，就能生成加密过的JPEG图像， 甚至不需要进行DCT变换。这个功能可以集成在网页中，用JavaScript即可实现。

附录：代码

本文用于实验的环境为GNU Octave 4.0.3，这里将用于产生各个例子的代码附加进来。

用于3.2的代码

clear;
pkg load signal;

lena = imread('lena512.pgm');
sizelena = size(lena);
width = sizelena(2);
height = sizelena(1);

lenadct = zeros(sizelena);
outputdct = zeros(sizelena);
output = zeros(sizelena);

% DCTize lena

for x = 1:8:height-1
    for y = 1:8:width-1
        lenadct(x:x+7, y:y+7) = dct2(lena(x:x+7, y:y+7));
        outputdct(x:x+7, y:y+7) = lenadct(x:x+7, y:y+7);
    endfor
endfor
    
% swap DCT parts

for x = 1:8:height-1
    for y = 1:8:width-1
        dx = height - x - 6;
        dy = width - y - 6;
        
        outputdct(dx:dx+1, dy:dy+1) = lenadct(x:x+1, y:y+1);
    endfor
endfor

% unDCTize output

for x = 1:8:height-1
    for y = 1:8:width-1
        output(x:x+7, y:y+7) = idct2(outputdct(x:x+7, y:y+7));
    endfor
endfor

imshow(uint8(output));

用于3.3的代码

代码包含两个部分，一个是用来生成随机排列的缓存文件的，一个是用来处理图像的。

randomize.m

randomize.m用于生成一组随机排列。 由于使用Octave只是为了验证思路，所以并没有使用密码算法来生成随机排列。

clear;

width = 64;
height = 64;
ptablelen = width*height;

ptable = zeros(64, ptablelen);
for i=1:192
    ptable(i, 1:ptablelen) = randperm(ptablelen);
endfor

save cache_ptable.mat ptable;
save cache_ptablelen.mat ptablelen;


i = 1;
destination = zeros(2, ptablelen);
for x = 1:8:width*8-1
    for y = 1:8:height*8-1
        destination(1:2,i) = [
            floor((i-1) / width) * 8 + 1;
            mod(i-1, width) * 8 + 1
        ];
        i += 1;
    endfor
endfor

save cache_destination.mat destination

encode.m / decode.m

encode.m 和 decode.m的区别就在于循环体中将矩阵参数搬运的顺序。见代码中的注释。

clear;
pkg load signal;

lena = imread('lena512.pgm');    % 读入文件的名称
outputname = 'output.jpg';       % 输出文件的名称
sizelena = size(lena);

lenadct = zeros(sizelena);

dest = zeros(sizelena);
destdct = zeros(sizelena);

load cache_ptable.mat;
load cache_ptablelen.mat;
load cache_destination.mat;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

p = 0;              % p: index of the random sequence used
chend = 3;
if size(size(lena)) < 3
    chend = 1;
endif

for ch = 1:chend        % iterate over RGB channels

    % DCTize lena

    for x = 1:8:512-1
        for y = 1:8:512-1
            lenadct(x:x+7, y:y+7, ch) = dct2(lena(x:x+7, y:y+7, ch));
            destdct(x:x+7, y:y+7, ch) = lenadct(x:x+7, y:y+7, ch);
        endfor
    endfor

    % permute DCT coefficients
    
    for oy=1:4:8
        for ox=1:4:8
            i = 1;
            p += 1;
            for x = 1:8:512-1
                for y = 1:8:512-1
                    di = ptable(p,i);
                    i += 1;
                    dx = destination(1, di);
                    dy = destination(2, di);
                    
                    % 下面两行，只能选取一行，另一行必须注释掉
                    destdct(dx+ox-1:dx+ox+2, dy+oy-1:dy+oy+2, ch) = lenadct(x+ox-1:x+ox+2, y+oy-1:y+oy+2, ch);    % 加密
                    % destdct(x+ox-1:x+ox+2, y+oy-1:y+oy+2, ch) = lenadct(dx+ox-1:dx+ox+2, dy+oy-1:dy+oy+2, ch);  % 解密
                endfor
            endfor
        endfor
    endfor

    % generate output

    for x = 1:8:512-1
        for y = 1:8:512-1
            dest(x:x+7, y:y+7, ch) = idct2(destdct(x:x+7, y:y+7, ch));
        endfor
    endfor
endfor  % for color channels

dest = uint8(dest);

imwrite(dest, outputname);