Merkle数字签名体制（MSS），是一种基于散列函数构建的数字签名算法，其优点在于不依赖可由量子计算机求解的某些问题而构建，因此具有在量子计算机出现后仍然足够安全的特点。本文意在根据作者的理解，介绍Merkle数字签名体制（Merkle Signature Scheme）的原理，以图分享新的消息和趋势。作者的身份只是对这类密码学问题感兴趣的业余爱好者，行文中定有用语或概念的问题，还请读者指正。

0. 散列函数

散列函数是一类函数，其允许任意长度的输入，但输出结果是固定长度。且理想的散列函数，从输出结果无法逆推输入。不仅是因为这是多对一的映射，还因为散列函数具有极强的非线性关系，使得输出的结果几乎是伪随机的。

对于确定的输入，散列函数给出确定的结果。对于这一输入，即使有微小的变化，散列函数的结果也会产生巨大的差异。散列函数一般用作对某些信息的“压缩”，使之可以在很大的概率上，唯一代表这类信息。

虽然散列函数无法逆推，但是仍然感兴趣，是否可以找到一种方法，寻找到满足某个输出结果的解。对于所有的散列函数，都至少存在一种“生日攻击”，即类似于“在同一间教室至少出现多少人，才能有>50%的概率，找到至少一对，其同月同日生”的问题。这一问题的解大约是散列函数的结果的空间的平方根的量级。例如对于生日问题（365），大约20人。对于一个输出结果长度为n比特的散列函数，在其输入数据中修改n/2个比特，就有一半的概率，找到一个同样的输出结果。

1. 数字签名

数字签名一般是这样的一种技术，用来使一个人向其他人在证明自己身份的同时证明自己确信某些其他的数据。这种技术的实现依赖一对数据，称为私钥和公钥。私钥是一个人保管的私有数据，公钥则公开传播。通过私钥和数字签名的算法，可以对一段确定的信息算出一个结果，称为签名。签名和信息是对应的，和私钥也是对应的。这一关系可以由公钥通过算法验证。

数字签名和手写的签名具有同样的目的：1、一个签名只能对应一个被签署的数据。验证签名不仅需要公钥，还需要输入被验证的数据。如果被验证的数据被篡改，则签名无法验证。2、由于和1类似的理由，虽然有同样的私钥，对于不同的数据产生的签名也是不同的。这样就不能将签名简单地复制而应用。3. 必须知道私钥，才可能根据算法产生签名。因此，只有私钥的所有者，才能产生签名。4. 签名一旦公布，任何人都可以使用公钥验证。签署者不能否认自己曾经签署过。

数字签名在技术上使得一个人可以通过不安全的、可能被篡改的通信方式（信道）通信时，仍然能证明自己的身份和自己的言论的完整性，避免伪造，避免冒充。对于接收人，可以保证签署人不能抵赖。

2. 抵抗量子计算机的签名算法

传统的签名算法有RSA、DSA等。这类算法因为原理上、数学上的原因，在量子计算机出现后将不再安全。然而量子计算机并非万能，仍然存在一类数学问题，对于量子计算机也是困难的。例如已知不可逆的散列函数的一个结果Y=H(X)，求其一个原像X0。Lamport一次签名就是利用这一原理构建的。

Lamport一次签名算法，对被签署的信息的每个比特进行签署。对于一个比特，选择两段和散列函数的输出等长的输入A和B作为私钥。A和B对应的散列结果H(A)和H(B)作为公钥。在签署时，如果比特是0, 就公布A，反之公布B。

以MD5为例，随机选择128段，每段长128比特的数据A1, A2, A3, ……A128，以及另128段数据B1, B2, B3, … B128, 作为私钥。对这些数据全部分别散列，公开H(A1), H(A2), H(A3), …, H(A128), H(B1), H(B2), H(B3), …, H(B128)，作为公钥。

当需要签署一段信息时，首先利用MD5对被签署的信息进行一次散列，得到被签署的信息，这样压缩了被签署的信息的长度至128比特。对于每个比特Bit1, Bit2, … Bit128，当其为1, 公布对应的B的值。反之，公布A。得到一个类似这样的组合：A1, B2, A3, A4, B5, A6, …, B128，即为签署结果。

显然，这种算法只能签署一次。因为一次的签署，已经泄漏了一半的私钥内容。如果再次进行签署，有很大的概率泄漏大部分的私钥。

3. 利用二叉树认证多个Lamport签名算法的公钥

为了签名，Lamport算法的公钥可以随意产生。我们希望找到一个方法，可以在利用数字签名之前，只和通信的对方交换一定的不变的数据，之后就利用这一数据验证我们选择的Lamport公钥。如果不进行某种验证，这种随意产生的公钥和身份认证之间就没有任何关系。

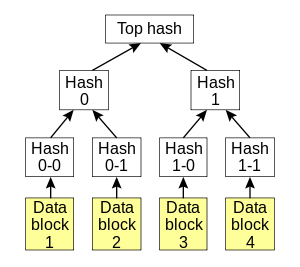
传统的MSS算法[1]，利用一个Merkle树，即一个完全二叉树，将一系列Lamport算法的公钥事先组合在一起。例如，我们事先产生16个Lamport公钥，编号1-16. 我们将之分组，(1,2), (3,4), (5,6), (7,8), (9,10), (11,12), (13, 14), (15, 16)。对于每组，例如（5,6），我们可以用散列函数计算它们混合后的一个摘要。这样就得到了8个值。继续将8个值分组，混合，散列，得到4个值……最后，我们在根上，得到一个值，这就是MSS树的公钥。它的长度等于一个散列函数的输出长度（几百比特，很小的）。

为了利用MSS树签名一个数据，我们需要首先选择一个它的叶子。在这个叶子上，利用对应的Lamport算法的私钥产生签名，然后公布签名和一次签名公钥。为了验证这个一次签名公钥属于我们的二叉树，我们在公布的签署结果中附加一个验证路径。它是那些必要的、将与Lamport一次签名公钥混合以便散列到根节点的值。在二叉树的每一层中都有一个这样的值。

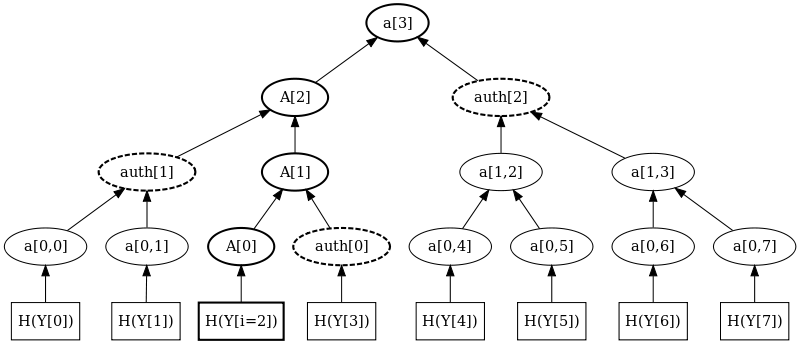
在上图中，Y[i=2]为一次签名的公钥。为了认证Y[i=2]，实际上是认证H(Y[i=2])，将它和auth[0], auth[1], auth[2]的结果一同公布。任何签名的验证者，将H(Y[i=2])和auth[j]依次混合，散列，最后可计算出一个根，其如果等于a[3]，即验证成功。

4. MSS树签名的缺点

如果不考虑缓存机制，为了得到一个很大的签名容量（即MSS树允许很多次的签署），我们就需要构建一个很大的MSS树。考虑一个20层的MSS树，其容量也不过2^20，即具有1048576个叶子。这对于一般的应用可能还是不够的。然而即使这样，我们为了计算验证路径，或者为了推导（根）公钥，在无缓存的情况下，将必须将整个树计算一遍，亦即计算1048576个叶子的散列，然后再经过1048575次混合的散列计算根。由于计算单个叶子的公钥，即使对于Lamport签名，其计算次数也正比于散列函数的输出比特的长度，所以一共的计算次数将是（2m+1)*2^n的样子，m是散列函数输出比特的长度，例如256或者512. n是树的层次，大概比如20. 这是极为耗时的。

即使为此选择使用缓存，在1048576（1M）的情况下，保存单个叶子的散列，也将导致比如64MByte的缓存（当m=256时）。仍然过于大了。

为了改进MSS树，增加签名容量并且加快速度，我们可以将多个MSS树串联。

5. 类似GMSS（通用MSS）的改进[2]

串联的意思是，我们在签署最终的用户输入的时候，使用一个层次比较小的树，比如4层。

为了验证这一小树的根公钥，我们用另一棵树的某个叶子，签署它的根公钥。如果我们选择5颗树，每棵树的层次为4层，一共仍然可以构建2^20次签名。这时，我们进行签名的代价是一棵4层树的代价×5. 大约正比于2^4，且远远小于2^20。

这样做的缺点是，将在签署结果中一次附加5棵树的签名。每个都是同样等于一个树签名的长度。这样结果就几乎扩大了5倍。可以说是用空间换取时间的方法。

这样做的优点是，节省了时间，并且可以预先计算树的一些参数。例如，为了产生根公钥，我们不需要在20层树上进行计算，只需要选择最顶层的一棵4层的树即可。因为各层树的根公钥是通过“签署”进行确认的，并无直接关系。

参考文献

[1] Ralph Merkle. A certified digital signature.

[2] Johannes Buchmann, Erik Dahmen, Elena Klintsevich. Merkle Signature with Virtually Unlimited Signature Capacity.

[3] Johannes Buchmann, Erik Dahmen, Andreas Huelsing. XMSS – A Practical Forward Secure Signature Scheme based on Minimal Security Assumptions.