受到某个论坛的作品启发,认为适时研究一下在计算机上表示三维图形是有必要的。原作品使用VB.Net+GDI绘图,我认为在要求不高的情况下用Python也不会有太难的解决方案。结果比想象的甚至还要简单。
解决方案是用python-visual这个模块。在Ubuntu 10.04下可以从软件源中安装。
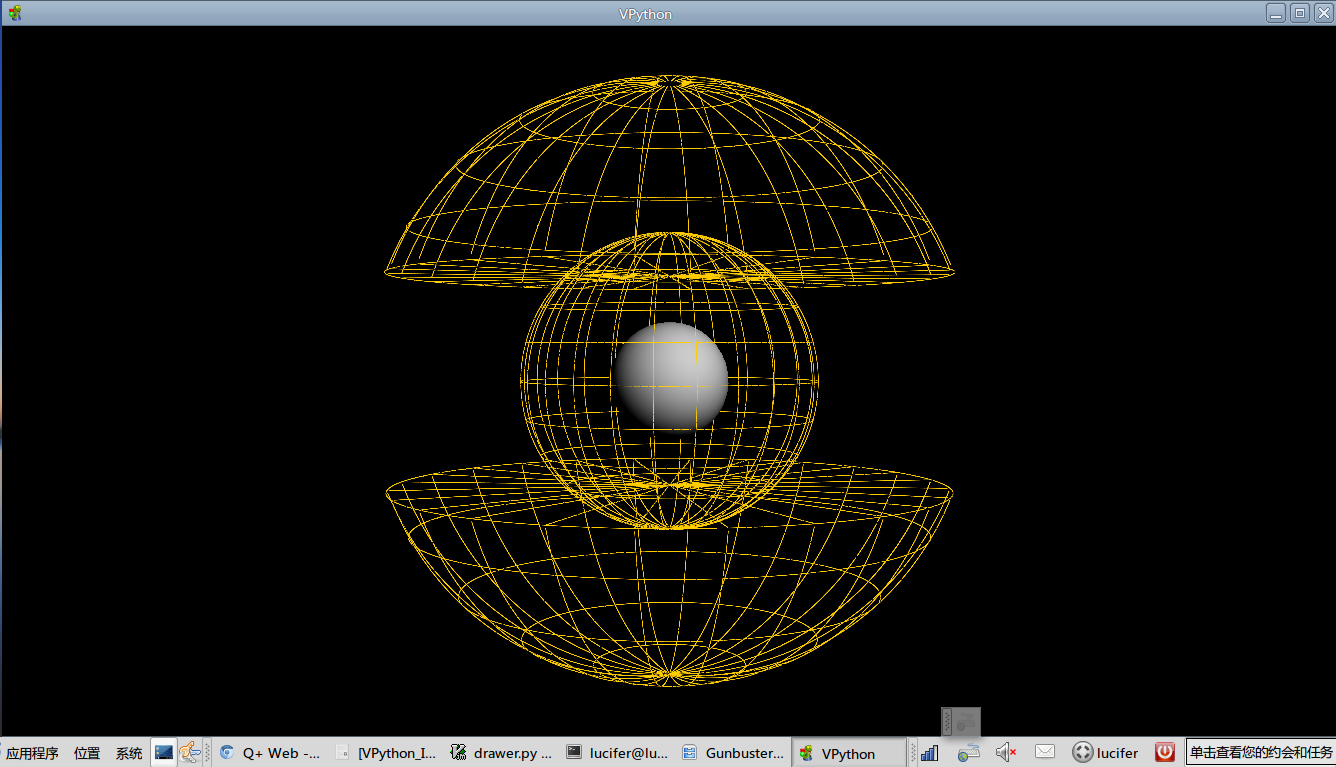
| 先放出我的示例程序,用来绘制GAINAX的动画《蓝宝石之谜》和《飞跃巅峰 | 》中出现过的一种三维图形(似乎是宇宙飞船的某种星体引力探测器屏幕)。 |
绘图思路:注意到本图主要由三种线构成——经线、纬线和半径线。在python-visual中,曲线有一个类:curve,根据输入的点(vector类)依次连线绘成,操作方法类似list的操作:
from visual import *
c = curve(color=color.yellow) # 指定颜色时,等价于 color=(1.0,1.0,0)
c.append(vector(0,0,0))
c.append(vector(0,1,0)) # 类似地画点在python-visual中,默认的坐标系定义为:以屏幕所在平面为xOy平面,向右为x轴,向上为y轴,垂直于屏幕向外为z轴。比例默认是自动调整的。当执行以上代码后,应该会弹出一个标题为VPython的画布。用鼠标右键可以调整坐标方向,滚轮按下后拉动鼠标调整缩放比例。
实现以上图形的完整代码如下,主要是数学运算,并不困难:
from visual import *
from math import *
# This will draw a graphic similar to The Secrets Of Blue Water's neo-nautilus navigation screen.
class screen(object):
magcircles = []
lngcircles = []
lines = []
def __init__(self):
self.color1 = (1.0,0.8,0)
self.centerball = sphere(pos=vector(0,0,0),radius=4,color=(0.5,0.5,0.5))
self.ballnet = self._ball(10)
def _ball(self,r):
R = 2.0 * r
dividangle = pi / 4
dividbeta = asin(r / R * sin(dividangle))
alpha = 0.0
while alpha < 2 * pi:
self.lngcircles.append(self._longitude(alpha,r,(-pi/2,pi/2)))# (-dividangle,dividangle)))
self.lngcircles.append(self._longitude(alpha,R, (-pi/2,-dividbeta)))
self.lngcircles.append(self._longitude(alpha,R, (dividbeta,pi/2)))
self.lines.append(
self._line(vector(0,r * sin(dividangle),0),
vector(R * cos(dividbeta) * cos(alpha),R * sin(dividbeta),R * cos(dividbeta) * sin(alpha)))
)
self.lines.append(
self._line(vector(0,-r * sin(dividangle),0),
vector(-R * cos(dividbeta) * cos(alpha),-R * sin(dividbeta),-R * cos(dividbeta) * sin(alpha)))
)
alpha += pi / 12
h_theta = - pi / 2
while h_theta < pi / 2:
if abs(h_theta) <= dividangle:
self.magcircles.append(self._magnitude(h_theta,r))
if abs(h_theta) >= dividbeta:
self.magcircles.append(self._magnitude(h_theta,R))
h_theta += pi / 12
self.magcircles.append(self._magnitude(dividbeta,R))
self.magcircles.append(self._magnitude(-dividbeta,R))
self.magcircles.append(self._magnitude(dividangle,r))
self.magcircles.append(self._magnitude(-dividangle,r))
def _line(self,p1,p2):
ret = curve(color=self.color1)
steps = 100
step = (p2 - p1) * 1.0 / steps
p = p1
for i in range(0,steps):
ret.append(p)
p += step
return ret
def _magnitude(self,beta,r):
ret = curve(color=self.color1)
theta = 0.0
d_theta = 0.05
while theta < 2 * pi:
ret.append(vector(r * cos(beta) * sin(theta),r * sin(beta),r * cos(beta) * cos(theta)))
theta += d_theta
return ret
def _longitude(self,alpha,r,anglerange=(-pi/2,pi/2)):
ret = curve(color=self.color1)
theta = -pi / 2
d_theta = 0.05
while theta < pi / 2:
if theta >= anglerange[0] and theta <= anglerange[1]:
ret.append(vector(r * cos(theta) * cos(alpha), r * sin(theta), r * cos(theta) * sin(alpha)))
theta += d_theta
return ret
s = screen()